Mekanika kuantum
Mekanika Kuantum atau QM, menjelaskan bagaimana alam semesta bekerja pada tingkat yang lebih kecil dari atom. Ini juga disebut "fisika kuantum" atau "teori kuantum". Kuantum adalah kata Latin untuk 'seberapa banyak', dan mekanika adalah bidang ilmu pengetahuan yang berkaitan dengan gerak. Kuantum energi adalah jumlah energi tertentu, dan Mekanika Kuantum menjelaskan bagaimana energi itu bergerak dan berinteraksi pada tingkat sub-atomik.
Atom dulunya dianggap sebagai blok bangunan terkecil dari materi, tetapi ilmu pengetahuan modern telah menunjukkan bahwa ada partikel yang lebih kecil lagi, seperti proton, neutron, dan elektron. QM adalah bagian dari fisika yang menjelaskan bagaimana partikel-partikel yang membentuk atom bekerja.
QM juga memberi tahu kita bagaimana gelombang elektromagnetik (seperti cahaya) bekerja. Banyak fisika dan kimia modern dapat dijelaskan dan dipahami dengan menggunakan aturan matematis mekanika Kuantum.
Matematika yang digunakan untuk mempelajari partikel subatomik dan gelombang elektromagnetik sangat kompleks, karena partikel-partikel tersebut bertindak dengan cara yang sangat aneh.
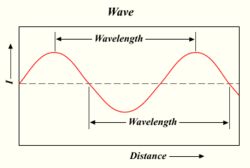
Panjang gelombang dari gelombang cahaya
Gelombang dan foton
Foton adalah partikel yang jauh lebih kecil daripada atom, proton dan elektron; bahkan, foton tidak memiliki massa sama sekali. Foton seperti "paket" atau paket energi. Sumber cahaya seperti lilin atau laser menembakkan (atau "memancarkan") cahaya dalam bit yang disebut foton.
Semakin banyak foton yang ditembakkan lampu, semakin terang cahayanya. Cahaya adalah bentuk energi yang berperilaku seperti gelombang dalam air atau gelombang radio. Jarak antara bagian atas satu gelombang dan bagian atas gelombang berikutnya disebut 'panjang gelombang'. Setiap foton membawa sejumlah tertentu, atau 'kuantum', energi tergantung pada panjang gelombangnya.
Warna cahaya tergantung pada panjang gelombangnya. Warna violet (warna paling bawah atau paling dalam dari pelangi) memiliki panjang gelombang sekitar 400 nm ("nanometer") yaitu 0,00004 sentimeter atau 0,000016 inci. Foton dengan panjang gelombang 10-400 nm disebut sinar ultraviolet (atau UV). Cahaya seperti itu tidak dapat dilihat oleh mata manusia. Di ujung spektrum yang lain, cahaya merah sekitar 700 nm. Cahaya inframerah sekitar 700 nm hingga 300.000 nm. Mata manusia juga tidak sensitif terhadap cahaya inframerah.
Panjang gelombang tidak selalu begitu kecil. Gelombang radio memiliki panjang gelombang yang lebih panjang. Panjang gelombang untuk radio FM bisa beberapa meter panjangnya (misalnya, stasiun yang mentransmisikan pada 99,5 FM memancarkan energi radio dengan panjang gelombang sekitar 3 meter, yaitu sekitar 10 kaki). Setiap foton memiliki sejumlah energi yang terkait dengan panjang gelombangnya. Semakin pendek panjang gelombang foton, semakin besar energinya. Misalnya, foton ultraviolet memiliki lebih banyak energi daripada foton inframerah.
Panjang gelombang dan frekuensi (berapa kali puncak gelombang per detik) berbanding terbalik, yang berarti panjang gelombang yang lebih panjang akan memiliki frekuensi yang lebih rendah, dan sebaliknya. Jika warna cahayanya inframerah (frekuensinya lebih rendah daripada cahaya merah), setiap foton dapat memanaskan apa yang dipukulnya. Jadi, jika lampu inframerah yang kuat (lampu panas) diarahkan ke seseorang, orang itu akan merasa hangat, atau bahkan panas, karena energi yang tersimpan dalam banyak foton. Permukaan lampu inframerah bahkan bisa menjadi cukup panas untuk membakar seseorang yang mungkin menyentuhnya. Manusia tidak dapat melihat cahaya inframerah, tetapi kita dapat merasakan radiasi dalam bentuk panas. Misalnya, seseorang yang berjalan di dekat bangunan batu bata yang telah dipanaskan oleh matahari akan merasakan panas dari bangunan tersebut tanpa harus menyentuhnya.
Formulasi matematis mekanika kuantum bersifat abstrak. Fungsi matematika, yang disebut fungsi gelombang, memberikan informasi tentang amplitudo probabilitas (kuadrat amplitudo probabilitas adalah probabilitas) dari posisi, momentum, dan sifat fisik lain dari sebuah partikel. Banyak hasil mekanika kuantum tidak mudah divisualisasikan dalam istilah mekanika klasik.
Sinar ultraviolet lebih tinggi frekuensinya daripada cahaya violet, sehingga bahkan tidak dalam kisaran cahaya tampak. Setiap foton dalam rentang ultraviolet memiliki banyak energi, cukup untuk melukai sel-sel kulit dan menyebabkan kulit terbakar. Faktanya, sebagian besar bentuk sengatan matahari tidak disebabkan oleh panas; mereka disebabkan oleh energi tinggi sinar UV matahari yang merusak sel-sel kulit Anda. Bahkan frekuensi cahaya yang lebih tinggi (atau radiasi elektromagnetik) dapat menembus lebih dalam ke dalam tubuh dan menyebabkan lebih banyak kerusakan. Sinar-X memiliki begitu banyak energi sehingga mereka dapat masuk jauh ke dalam tubuh manusia dan membunuh sel. Manusia tidak dapat melihat atau merasakan sinar ultraviolet atau sinar-x. Mereka mungkin hanya tahu bahwa mereka telah berada di bawah cahaya frekuensi tinggi seperti itu ketika mereka mendapatkan luka bakar radiasi. Area di mana penting untuk membunuh kuman sering menggunakan lampu ultraviolet untuk menghancurkan bakteri, jamur, dll. Sinar-X kadang-kadang digunakan untuk membunuh sel-sel kanker.
Mekanika kuantum dimulai ketika ditemukan bahwa frekuensi tertentu berarti sejumlah energi tertentu. Energi sebanding dengan frekuensi (E ∝ f). Semakin tinggi frekuensinya, semakin banyak energi yang dimiliki foton, dan semakin banyak kerusakan yang dapat dilakukannya. Mekanika kuantum kemudian berkembang untuk menjelaskan struktur internal atom. Mekanika kuantum juga menjelaskan cara foton dapat mengganggu dirinya sendiri, dan banyak hal lain yang tidak pernah dibayangkan dalam fisika klasik.

Hitam di kiri adalah ultraviolet (frekuensi tinggi); hitam di kanan adalah inframerah (frekuensi rendah).
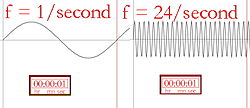
Deskripsi bergambar tentang frekuensi
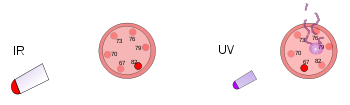
Di sebelah kiri, termometer plastik berada di bawah lampu panas yang terang. Radiasi inframerah ini menghangatkan tetapi tidak merusak termometer. Di sebelah kanan, termometer plastik lainnya terkena sinar ultraviolet intensitas rendah. Radiasi ini merusak tetapi tidak menghangatkan termometer.
Kuantisasi
Max Planck menemukan hubungan antara frekuensi dan energi. Tidak ada seorang pun sebelumnya yang pernah menduga bahwa frekuensi berbanding lurus dengan energi (ini berarti bahwa ketika salah satu dari keduanya berlipat ganda, yang lain juga demikian). Di bawah apa yang disebut satuan alami, maka angka yang mewakili frekuensi foton juga akan mewakili energinya. Maka persamaannya adalah:
E = f
yang berarti energi sama dengan frekuensi.
Tetapi cara fisika berkembang, tidak ada hubungan alami antara unit yang digunakan untuk mengukur energi dan unit yang biasa digunakan untuk mengukur waktu (dan karenanya frekuensi). Jadi rumus yang Planck kerjakan untuk membuat angka-angka itu keluar dengan benar adalah:
E = h × f
atau, energi sama dengan h kali frekuensi. H ini adalah angka yang disebut konstanta Planck sesuai dengan nama penemunya.
Mekanika kuantum didasarkan pada pengetahuan bahwa foton dengan frekuensi tertentu berarti foton dengan jumlah energi tertentu. Selain hubungan itu, jenis atom tertentu hanya dapat mengeluarkan frekuensi radiasi tertentu, sehingga ia juga hanya dapat mengeluarkan foton yang memiliki jumlah energi tertentu.
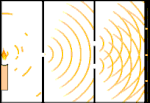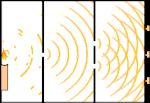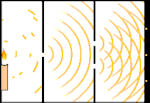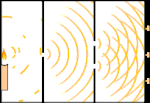
Eksperimen celah ganda: cahaya bergerak dari sumber cahaya di sebelah kiri ke pinggiran (ditandai di tepi hitam) di sebelah kanan.
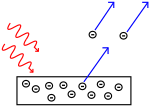
Efek fotolistrik: foton mengenai logam dan elektron terdorong menjauh.
Sejarah
Isaac Newton berpikir bahwa cahaya terbuat dari benda-benda yang sangat kecil yang sekarang kita sebut partikel (dia menyebutnya sebagai "Corpuscles"). Christiaan Huygens berpikir bahwa cahaya terbuat dari gelombang. Para ilmuwan berpikir bahwa sesuatu tidak bisa menjadi partikel dan gelombang pada saat yang sama.
Para ilmuwan melakukan eksperimen untuk mengetahui apakah cahaya terbuat dari partikel atau gelombang. Mereka menemukan bahwa kedua gagasan itu benar - cahaya entah bagaimana merupakan gelombang dan partikel. Eksperimen celah ganda yang dilakukan oleh Thomas Young menunjukkan bahwa cahaya harus bertindak seperti gelombang. Efek fotolistrik yang ditemukan oleh Albert Einstein membuktikan bahwa cahaya harus bertindak seperti partikel yang membawa sejumlah energi tertentu, dan bahwa energi tersebut terkait dengan frekuensinya. Hasil eksperimen ini disebut "dualitas gelombang-partikel" dalam mekanika kuantum. Kemudian, fisikawan menemukan bahwa segala sesuatu berperilaku seperti gelombang dan partikel, bukan hanya cahaya. Namun, efek ini jauh lebih kecil pada benda-benda besar.
Berikut ini adalah beberapa orang yang menemukan bagian-bagian dasar mekanika kuantum: Max Planck, Albert Einstein, Satyendra Nath Bose, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, John von Neumann, dan Richard Feynman. Mereka melakukan pekerjaan mereka pada paruh pertama abad ke-20.

Kiri ke kanan: Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, Richard Feynman.
Di luar Planck
Rumus dan gagasan mekanika kuantum dibuat untuk menjelaskan cahaya yang berasal dari hidrogen yang bercahaya. Teori kuantum atom juga harus menjelaskan mengapa elektron tetap berada di orbitnya, yang tidak dapat dijelaskan oleh gagasan lain. Ini mengikuti dari ide-ide yang lebih tua bahwa elektron harus jatuh ke pusat atom karena ia mulai dijaga di orbit oleh energinya sendiri, tetapi dengan cepat akan kehilangan energinya saat ia berputar di orbitnya. (Ini karena elektron dan partikel bermuatan lainnya diketahui memancarkan cahaya dan kehilangan energi ketika mereka mengubah kecepatan atau berbelok).
Lampu hidrogen bekerja seperti lampu neon, tetapi lampu neon memiliki kelompok warna (dan frekuensi) cahayanya sendiri yang unik. Para ilmuwan mengetahui bahwa mereka bisa mengidentifikasi semua elemen dari warna cahaya yang mereka hasilkan. Mereka hanya tidak tahu bagaimana frekuensi ditentukan.
Kemudian, seorang matematikawan Swiss bernama Johann Balmer menemukan persamaan yang memberi tahu berapa λ (lambda, untuk panjang gelombang):
λ = B ( n 2 n 2 - 4 ) n = 3 , 4 , 5 , 6 {\displaystyle \lambda =B\kiri({\frac {n^{{2}}{n^{2}-4}}}\kanan)\qquad \qquad n=3,4,5,6}
di mana B adalah angka yang ditentukan Balmer sama dengan 364,56 nm.
Persamaan ini hanya bekerja untuk cahaya tampak dari lampu hidrogen. Tetapi kemudian, persamaan itu dibuat lebih umum:
1 λ = R ( 1 m 2 - 1 n 2 ) , {\displaystyle {\frac {1}{{\lambda }}=R\left({\frac {1}{m^{2}}}}-{\frac {1}{n^{2}}}}}}}}}\right),}
di mana R adalah konstanta Rydberg, sama dengan 0,0110 nm−1 , dan n harus lebih besar dari m.
Dengan memasukkan angka-angka yang berbeda untuk m dan n, mudah untuk memprediksi frekuensi untuk banyak jenis cahaya (ultraviolet, tampak, dan infared). Untuk melihat bagaimana cara kerjanya, buka Hyperphysics dan turun melewati bagian tengah halaman. (Gunakan H = 1 untuk hidrogen).
Pada tahun 1908, Walter Ritz membuat prinsip kombinasi Ritz yang menunjukkan bagaimana celah tertentu di antara frekuensi terus berulang. Hal ini ternyata penting bagi Werner Heisenberg beberapa tahun kemudian.
Pada tahun 1905, Albert Einstein menggunakan ide Planck untuk menunjukkan bahwa seberkas cahaya terdiri dari aliran partikel yang disebut foton. Energi setiap foton tergantung pada frekuensinya. Gagasan Einstein adalah awal dari gagasan dalam mekanika kuantum bahwa semua partikel subatomik seperti elektron, proton, neutron, dan lainnya adalah gelombang dan partikel pada saat yang sama. (Lihat gambar atom dengan elektron sebagai gelombang pada atom.) Hal ini menyebabkan teori tentang partikel subatomik dan gelombang elektromagnetik yang disebut dualitas gelombang-partikel. Di sinilah partikel dan gelombang tidak satu atau yang lain, tetapi memiliki sifat tertentu dari keduanya.
Pada tahun 1913, Niels Bohr muncul dengan gagasan bahwa elektron hanya dapat mengambil orbit tertentu di sekitar inti atom. Di bawah teori Bohr, angka-angka yang disebut m dan n dalam persamaan di atas dapat mewakili orbit. Teori Bohr mengatakan elektron bisa mulai di beberapa orbit m dan berakhir di beberapa orbit n, atau elektron bisa mulai di beberapa orbit n dan berakhir di beberapa orbit m jadi jika sebuah foton mengenai elektron, energinya akan diserap, dan elektron akan pindah ke orbit yang lebih tinggi karena energi ekstra itu. Berdasarkan teori Bohr, jika elektron jatuh dari orbit yang lebih tinggi ke orbit yang lebih rendah, maka elektron harus menyerahkan energi dalam bentuk foton. Energi foton akan sama dengan perbedaan energi antara kedua orbit, dan energi foton membuatnya memiliki frekuensi dan warna tertentu. Teori Bohr memberikan penjelasan yang baik tentang banyak aspek fenomena subatomik, tetapi gagal menjawab mengapa masing-masing warna cahaya yang dihasilkan oleh hidrogen yang bercahaya (dan oleh neon yang bercahaya atau elemen lainnya) memiliki kecerahannya sendiri, dan perbedaan kecerahan selalu sama untuk setiap elemen.
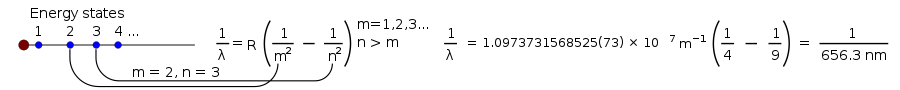
Pada saat Niels Bohr mengeluarkan teorinya, sebagian besar hal tentang cahaya yang dihasilkan oleh lampu hidrogen sudah diketahui, tetapi para ilmuwan masih belum bisa menjelaskan kecerahan setiap garis yang dihasilkan oleh hidrogen yang bersinar.
Werner Heisenberg mengambil tugas untuk menjelaskan kecerahan atau "intensitas" dari setiap garis. Dia tidak bisa menggunakan aturan sederhana seperti yang dibuat oleh Balmer. Dia harus menggunakan matematika fisika klasik yang sangat sulit yang menghitung semuanya dalam hal hal-hal seperti massa (berat) elektron, muatan (kekuatan listrik statis) elektron, dan jumlah kecil lainnya. Fisika klasik sudah memiliki jawaban untuk kecerahan pita warna yang dihasilkan lampu hidrogen, tetapi teori klasik mengatakan bahwa harus ada pelangi yang berkelanjutan, dan bukan empat pita warna yang terpisah. Penjelasan Heisenberg adalah:
Ada beberapa hukum yang mengatakan frekuensi cahaya apa yang akan dihasilkan oleh hidrogen yang bercahaya. Ini harus memprediksi frekuensi yang berjarak ketika elektron yang terlibat bergerak di antara orbit yang dekat dengan inti (pusat) atom, tetapi juga harus memprediksi bahwa frekuensi akan semakin dekat dan lebih dekat bersama ketika kita melihat apa yang dilakukan elektron dalam bergerak di antara orbit semakin jauh dan semakin jauh keluar. Ini juga akan memprediksi bahwa perbedaan intensitas antara frekuensi semakin dekat dan semakin dekat bersama saat kita keluar. Ketika fisika klasik sudah memberikan jawaban yang benar dengan satu set persamaan, fisika baru harus memberikan jawaban yang sama tetapi dengan persamaan yang berbeda.
Fisika klasik menggunakan metode matematikawan Prancis Fourier untuk membuat gambaran matematika dari dunia fisik, dan menggunakan kumpulan kurva halus yang menyatu untuk membuat satu kurva halus yang memberikan, dalam hal ini, intensitas untuk cahaya dari semua frekuensi dari beberapa cahaya. Tapi itu tidak benar karena kurva halus itu hanya muncul pada frekuensi yang lebih tinggi. Pada frekuensi yang lebih rendah, selalu ada titik-titik yang terisolasi dan tidak ada yang menghubungkan titik-titik tersebut. Jadi, untuk membuat peta dunia nyata, Heisenberg harus membuat perubahan besar. Dia harus melakukan sesuatu untuk memilih hanya angka-angka yang cocok dengan apa yang terlihat di alam. Kadang-kadang orang mengatakan dia "menebak" persamaan-persamaan ini, tetapi dia tidak membuat tebakan buta. Dia menemukan apa yang dia butuhkan. Angka-angka yang dia hitung akan menempatkan titik-titik pada grafik, tetapi tidak akan ada garis yang ditarik di antara titik-titik itu. Dan membuat satu "grafik" hanya dari titik-titik untuk setiap rangkaian perhitungan akan membuang banyak kertas dan tidak akan menyelesaikan apa pun. Heisenberg menemukan cara untuk memprediksi intensitas secara efisien untuk frekuensi yang berbeda dan untuk mengatur informasi itu dengan cara yang bermanfaat.
Hanya dengan menggunakan aturan empiris yang diberikan di atas, aturan yang dimulai oleh Balmer dan diperbaiki oleh Rydberg, kita dapat melihat bagaimana mendapatkan satu set angka yang akan membantu Heisenberg mendapatkan jenis gambar yang diinginkannya:
Aturannya mengatakan bahwa ketika elektron bergerak dari satu orbit ke orbit lainnya, ia akan memperoleh atau kehilangan energi, tergantung pada apakah ia semakin jauh dari pusat atau lebih dekat dengannya. Jadi, kita dapat menempatkan orbit atau tingkat energi ini sebagai judul di sepanjang bagian atas dan samping kisi. Untuk alasan historis, orbit terendah disebut n, dan orbit berikutnya disebut n - a, kemudian muncul n - b, dan seterusnya. Memang membingungkan bahwa mereka menggunakan angka negatif ketika elektron sebenarnya mendapatkan energi, tetapi begitulah adanya.
Karena aturan Rydberg memberi kita frekuensi, kita dapat menggunakan aturan itu untuk memasukkan angka tergantung ke mana elektron pergi. Jika elektron mulai dari n dan berakhir di n, maka elektron tidak benar-benar pergi ke mana pun, jadi ia tidak mendapatkan energi dan tidak kehilangan energi. Jadi frekuensinya adalah 0. Jika elektron mulai dari n-a dan berakhir di n, maka ia telah jatuh dari orbit yang lebih tinggi ke orbit yang lebih rendah. Jika hal itu terjadi, maka ia kehilangan energi, dan energi yang hilang muncul sebagai foton. Foton memiliki sejumlah energi, e, dan itu terkait dengan frekuensi tertentu f dengan persamaan e = h f. Jadi kita tahu bahwa perubahan orbit tertentu akan menghasilkan frekuensi cahaya tertentu, f. Jika elektron mulai dari n dan berakhir di n - a, itu berarti ia telah berpindah dari orbit yang lebih rendah ke orbit yang lebih tinggi. Itu hanya terjadi ketika foton dengan frekuensi dan energi tertentu masuk dari luar, diserap oleh elektron dan memberinya energi, dan itulah yang membuat elektron keluar ke orbit yang lebih tinggi. Jadi, agar semuanya masuk akal, kita menulis frekuensi itu sebagai angka negatif. Ada foton dengan frekuensi tertentu dan sekarang telah diambil.
Jadi kita bisa membuat kisi-kisi seperti ini, di mana f(a←b) berarti frekuensi yang terlibat ketika elektron berpindah dari keadaan energi (orbit) b ke keadaan energi a (Sekali lagi, urutannya terlihat terbalik, tetapi begitulah cara awalnya ditulis.):
Kisi-kisi dari f
| Keadaan Elektron | n | n-a | n-b | n-c | .... | |
| n | f(n←n) | f(n←n-a) | f(n←n-b) | f(n←n-c) | ..... | |
| n-a | f(n-a←n) | f(n-a←n-a) | f(n-a←n-b) | f(n-a←n-c) | ..... | |
| n-b | f(n-b←n) | f(n-b←n-a) | f(n-b←n-b) | f(n-b←n-c) | ..... | |
| transisi.... | ..... | ..... | ..... | ..... |
Heisenberg tidak membuat kisi-kisi seperti ini. Dia hanya melakukan perhitungan yang memungkinkannya mendapatkan intensitas yang dia cari. Tetapi untuk melakukan itu, dia harus mengalikan dua amplitudo (seberapa tinggi ukuran gelombang) untuk mengetahui intensitasnya. (Dalam fisika klasik, intensitas sama dengan amplitudo kuadrat.) Dia membuat persamaan yang tampak aneh untuk menangani masalah ini, menulis sisa makalahnya, menyerahkannya kepada atasannya, dan pergi berlibur. Dr. Born melihat persamaan lucunya dan itu tampak sedikit gila. Dia pasti bertanya-tanya, "Mengapa Heisenberg memberi saya hal yang aneh ini? Mengapa dia harus melakukannya dengan cara ini?" Kemudian dia menyadari bahwa dia sedang melihat cetak biru untuk sesuatu yang sudah dia ketahui dengan sangat baik. Dia terbiasa menyebut kisi-kisi atau tabel yang bisa kita tulis dengan melakukan, misalnya, semua matematika untuk frekuensi, matriks. Dan persamaan aneh Heisenberg adalah aturan untuk mengalikan dua dari mereka bersama-sama. Max Born adalah seorang matematikawan yang sangat, sangat baik. Dia tahu bahwa karena dua matriks (kisi-kisi) yang dikalikan mewakili hal-hal yang berbeda (seperti posisi (x,y,z) dan momentum (mv), misalnya), maka ketika Anda mengalikan matriks pertama dengan matriks kedua, Anda akan mendapatkan satu jawaban, dan ketika Anda mengalikan matriks kedua dengan matriks pertama, Anda akan mendapatkan jawaban yang lain. Meskipun dia tidak tahu tentang matematika matriks, Heisenberg sudah melihat masalah "jawaban yang berbeda" ini dan itu telah mengganggunya. Born adalah seorang matematikawan yang baik sehingga dia melihat bahwa perbedaan antara perkalian matriks pertama dan perkalian matriks kedua selalu akan melibatkan konstanta Planck, h, dikalikan dengan akar kuadrat dari negatif satu, i. Jadi dalam beberapa hari setelah penemuan Heisenberg, mereka sudah memiliki matematika dasar untuk apa yang Heisenberg suka menyebutnya "prinsip ketidakpastian". Dengan "tak tentu" Heisenberg berarti bahwa sesuatu seperti elektron tidak dijepit sampai dijepit. Ini sedikit seperti ubur-ubur yang selalu meremas-remas dan tidak bisa "di satu tempat" kecuali Anda membunuhnya. Belakangan, orang terbiasa menyebutnya "prinsip ketidakpastian Heisenberg," yang membuat banyak orang membuat kesalahan dengan berpikir bahwa elektron dan hal-hal seperti itu benar-benar "ada di suatu tempat" tetapi kita hanya tidak yakin tentang hal itu dalam pikiran kita sendiri. Gagasan itu salah. Bukan itu yang dibicarakan Heisenberg. Mengalami kesulitan mengukur sesuatu adalah masalah, tetapi itu bukan masalah yang dibicarakan Heisenberg.
Gagasan Heisenberg sangat sulit dipahami, tetapi kita dapat membuatnya lebih jelas dengan sebuah contoh. Pertama, kita akan mulai menyebut kisi-kisi ini sebagai "matriks," karena kita akan segera perlu berbicara tentang perkalian matriks.
Misalkan kita mulai dengan dua jenis pengukuran, posisi (q) dan momentum (p). Pada tahun 1925, Heisenberg menulis persamaan seperti ini:
Y ( n , n - b ) = ∑ a p ( n , n - a ) q ( n - a , n - b ) {\displaystyle Y(n,n - b)=\sum _{a}^{}}\,p(n,n - a)q(n - a,n - b)}
Dia tidak mengetahuinya, tetapi persamaan ini memberikan cetak biru untuk menuliskan dua matriks (kisi-kisi) dan untuk mengalikannya. Aturan untuk mengalikan satu matriks dengan matriks lainnya sedikit berantakan, tetapi berikut ini adalah dua matriks menurut cetak biru tersebut, dan kemudian hasil kalinya:
Matriks dari p
| Keadaan Elektron | n-a | n-b | n-c | .... | |
| n | p(n←n-a) | p(n←n-b) | p(n←n-c) | ..... | |
| n-a | p(n-a←n-a) | p(n-a←n-b) | p(n-a←n-c) | ..... | |
| n-b | p(n-b←n-a) | p(n-b←n-b) | p(n-b←n-c) | ..... | |
| transisi.... | ..... | ..... | ..... | ..... |
Matriks dari q
| Keadaan Elektron | n-b | n-c | n-d | .... | |
| n-a | q(n-a←n-b) | q(n-a←n-c) | q(n-a←n-d) | ..... | |
| n-b | q(n-b←n-b) | q(n-b←n-c) | q(n-b←n-d) | ..... | |
| n-c | q(n-c←n-b) | q(n-c←n-c) | q(n-c←n-d) | ..... | |
| transisi.... | ..... | ..... | ..... | ..... |
Matriks untuk hasil kali dua matriks di atas seperti yang ditentukan oleh persamaan yang relevan dalam makalah Heisenberg tahun 1925 adalah:
| Keadaan Elektron | n-b | n-c | n-d | ..... |
| n | A | ..... | ..... | ..... |
| n-a | ..... | B | ..... | ..... |
| n-b | ..... | ..... | C | ..... |
Di mana:
A=p(n←n-a)*q(n-a←n-b)+p(n←n-b)*q(n-b←n-b)+p(n←n-c)*q(n-c←n-b)+.....
B=p(n-a←n-a)*q(n-a←n-c)+p(n-a←n-b)*q(n-b←n-c)+p(n-a←n-c)*q(n-c←n-c)+.....
C=p(n-b←n-a)*q(n-a←n-d)+p(n-b←n-b)*q(n-b←n-d)+p(n-b←n-c)*q(n-d←n-d)+.....
dan sebagainya.
Jika matriks-matriks itu dibalik, nilai-nilai berikut ini akan dihasilkan:
A=q(n←n-a)*p(n-a←n-b)+q(n←n-b)*p(n-b←n-b)+q(n←n-c)*p(n-c←n-b)+.....
B=q(n-a←n-a)*p(n-a←n-c)+q(n-a←n-b)*p(n-b←n-c)+q(n-a←n-c)*p(n-c←n-c)+.....
C=q(n-b←n-a)*p(n-a←n-d)+q(n-b←n-b)*p(n-b←n-d)+q(n-b←n-c)*p(n-d←n-d)+.....
dan sebagainya.
Perhatikan bagaimana mengubah urutan perkalian mengubah angka-angka, langkah demi langkah, yang sebenarnya dikalikan.

Cahaya tampak yang dipancarkan oleh hidrogen yang bersinar. (Panjang gelombang dalam nanometer.)
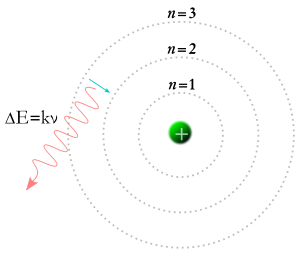
Elektron jatuh ke orbit yang lebih rendah dan foton tercipta.
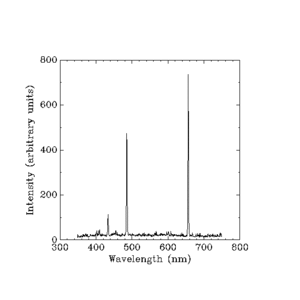
Intensitas yang berjarak dalam unit arbitrer
Di luar Heisenberg
Karya Werner Heisenberg tampaknya memecah kemacetan. Tak lama kemudian, banyak cara lain yang berbeda untuk menjelaskan berbagai hal datang dari orang-orang seperti Louis de Broglie, Max Born, Paul Dirac, Wolfgang Pauli, dan Erwin Schrödinger. Karya masing-masing fisikawan ini adalah kisahnya sendiri. Matematika yang digunakan oleh Heisenberg dan orang-orang sebelumnya tidak terlalu sulit untuk dipahami, tetapi persamaan-persamaan dengan cepat tumbuh sangat rumit ketika fisikawan melihat lebih dalam ke dunia atom.
Misteri lebih lanjut
Pada masa-masa awal mekanika kuantum, Albert Einstein menyarankan bahwa jika mekanika kuantum benar, maka mekanika kuantum akan berarti bahwa akan ada "aksi seram di kejauhan". Ternyata mekanika kuantum benar, dan bahwa apa yang Einstein gunakan sebagai alasan untuk menolak mekanika kuantum benar-benar terjadi. "Hubungan seram" antara peristiwa-peristiwa kuantum tertentu ini sekarang disebut "quantum entanglement".
Ketika sebuah eksperimen menyatukan dua hal (foton, elektron, dll.), mereka kemudian harus berbagi deskripsi umum dalam mekanika kuantum. Ketika mereka kemudian dipisahkan, mereka mempertahankan deskripsi mekanika kuantum yang sama atau "keadaan". Dalam diagram, satu karakteristik (misalnya, spin "atas") digambar dengan warna merah, dan pasangannya (misalnya, spin "bawah") digambar dengan warna biru. Pita ungu berarti bahwa ketika, misalnya, dua elektron disatukan, pasangan tersebut berbagi kedua karakteristik. Jadi kedua elektron bisa menunjukkan spin atas atau spin bawah. Ketika mereka kemudian dipisahkan, yang satu tetap di Bumi dan yang satu pergi ke suatu planet bintang Alpha Centauri, masing-masing masih memiliki kedua spin. Dengan kata lain, masing-masing dari mereka dapat "memutuskan" untuk menunjukkan dirinya sebagai elektron spin-up atau elektron spin-down. Tetapi, jika kemudian seseorang mengukur elektron yang satunya lagi, maka elektron itu harus "memutuskan" untuk menunjukkan dirinya sebagai elektron yang memiliki spin yang berlawanan.
Einstein berargumen bahwa dalam jarak yang begitu jauh, adalah gila untuk berpikir bahwa memaksa satu elektron untuk menunjukkan spinnya kemudian entah bagaimana akan membuat elektron lainnya menunjukkan karakteristik yang berlawanan. Dia mengatakan bahwa kedua elektron pasti spin-up atau spin-down selama ini, tetapi mekanika kuantum tidak dapat memprediksi karakteristik mana yang dimiliki setiap elektron. Karena tidak dapat memprediksi, hanya mampu melihat salah satunya dengan eksperimen yang tepat, berarti mekanika kuantum tidak dapat menjelaskan sesuatu yang penting. Oleh karena itu, kata Einstein, mekanika kuantum memiliki lubang besar di dalamnya. Mekanika kuantum tidak lengkap.
Belakangan, ternyata eksperimen menunjukkan bahwa Einstein-lah yang salah.
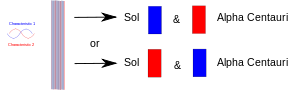
Dua partikel terjerat dipisahkan: satu di Bumi dan satu lagi dibawa ke planet yang jauh. Mengukur salah satu dari mereka memaksanya untuk "memutuskan" peran mana yang akan diambil, dan yang lain kemudian harus mengambil peran lain kapan pun (setelah itu) diukur.
Prinsip ketidakpastian Heisenberg
Pada tahun 1925, Werner Heisenberg menjelaskan prinsip Ketidakpastian, yang mengatakan bahwa semakin banyak kita tahu tentang di mana suatu partikel berada, semakin sedikit kita bisa tahu tentang seberapa cepat partikel itu bergerak dan ke arah mana. Dengan kata lain, semakin banyak kita tahu tentang kecepatan dan arah sesuatu yang kecil, semakin sedikit kita bisa tahu tentang posisinya. Fisikawan biasanya berbicara tentang momentum dalam diskusi semacam itu alih-alih berbicara tentang kecepatan. Momentum hanyalah kecepatan sesuatu dalam arah tertentu dikalikan massanya.
Alasan di balik prinsip ketidakpastian Heisenberg mengatakan bahwa kita tidak akan pernah bisa mengetahui lokasi dan momentum suatu partikel. Karena cahaya adalah partikel yang berlimpah, maka cahaya digunakan untuk mengukur partikel lain. Satu-satunya cara untuk mengukurnya adalah dengan memantulkan gelombang cahaya dari partikel dan mencatat hasilnya. Jika sinar cahaya berenergi tinggi, atau frekuensi tinggi, digunakan, kita dapat mengetahui dengan tepat di mana ia berada, tetapi tidak dapat mengetahui seberapa cepat ia bergerak. Ini karena foton energi tinggi mentransfer energi ke partikel dan mengubah kecepatan partikel. Jika kita menggunakan foton berenergi rendah, kita dapat mengetahui seberapa cepat partikel itu bergerak, tetapi tidak dapat mengetahui di mana partikel itu berada. Ini karena kita menggunakan cahaya dengan panjang gelombang yang lebih panjang. Panjang gelombang yang lebih panjang berarti partikel bisa berada di mana saja di sepanjang bentangan gelombang.
Prinsip ini juga mengatakan bahwa ada banyak pasangan pengukuran yang kita tidak dapat mengetahui keduanya tentang partikel apa pun (hal yang sangat kecil), tidak peduli seberapa keras kita mencoba. Semakin banyak kita belajar tentang salah satu dari pasangan tersebut, semakin sedikit yang bisa kita ketahui tentang pasangan yang lain.
Bahkan Albert Einstein mengalami kesulitan menerima konsep aneh seperti itu, dan dalam sebuah debat terkenal mengatakan, "Tuhan tidak bermain dadu". Terhadap hal ini, fisikawan Denmark Niels Bohr dengan terkenal menjawab, "Einstein, jangan katakan kepada Tuhan apa yang harus dilakukan".
Penggunaan QM
Elektron mengelilingi setiap inti atom. Ikatan kimia menghubungkan atom-atom untuk membentuk molekul. Ikatan kimia menghubungkan dua atom ketika elektron dibagi di antara atom-atom itu. Jadi QM adalah fisika dari ikatan kimia dan kimia. QM membantu kita memahami bagaimana molekul dibuat, dan apa sifat-sifatnya.
QM juga dapat membantu kita memahami benda-benda besar, seperti bintang dan bahkan seluruh alam semesta. QM adalah bagian yang sangat penting dari teori bagaimana alam semesta dimulai yang disebut Big Bang.
Segala sesuatu yang terbuat dari materi tertarik ke materi lain karena gaya fundamental yang disebut gravitasi. Teori Einstein yang menjelaskan gravitasi disebut teori relativitas umum. Masalah dalam fisika modern adalah bahwa beberapa kesimpulan QM tampaknya tidak sesuai dengan teori relativitas umum.
QM adalah bagian dari fisika yang dapat menjelaskan mengapa semua teknologi elektronik bekerja seperti itu. Jadi QM menjelaskan bagaimana komputer bekerja, karena komputer adalah mesin elektronik. Tetapi para perancang perangkat keras komputer awal sekitar tahun 1950 atau 1960 tidak perlu memikirkan QM. Para perancang radio dan televisi pada waktu itu juga tidak memikirkan QM. Namun, desain sirkuit terpadu yang lebih kuat dan teknologi memori komputer beberapa tahun terakhir ini memang memerlukan QM.
QM juga telah memungkinkan teknologi seperti:
- Spektroskopi
- Laser
- MRI
- CD dan DVD
Mengapa QM sulit dipelajari
QM adalah subjek yang menantang karena beberapa alasan:
- QM menjelaskan berbagai hal dengan cara yang sangat berbeda dari apa yang kita pelajari tentang dunia ketika kita masih anak-anak.
- Memahami QM membutuhkan lebih banyak matematika daripada aljabar dan kalkulus sederhana. Ini juga membutuhkan aljabar matriks, bilangan kompleks, teori probabilitas, dan persamaan diferensial parsial.
- Fisikawan tidak yakin apa yang dikatakan beberapa persamaan QM tentang dunia nyata.
- QM menunjukkan bahwa atom dan partikel subatom berperilaku aneh, sama sekali tidak seperti apa pun yang kita lihat dalam kehidupan kita sehari-hari.
- QM menggambarkan hal-hal yang sangat kecil, sehingga kita tidak dapat melihat beberapa di antaranya tanpa peralatan khusus, dan kita tidak dapat melihat banyak di antaranya sama sekali.
QM menggambarkan alam dengan cara yang berbeda dari cara kita biasanya berpikir tentang sains. QM memberitahu kita seberapa besar kemungkinan terjadinya beberapa hal, daripada memberitahu kita bahwa hal itu pasti akan terjadi.
Salah satu contohnya adalah eksperimen celah ganda Young. Jika kita menembakkan foton tunggal (unit cahaya tunggal) dari laser pada selembar film fotografi, kita akan melihat satu titik cahaya pada film yang dikembangkan. Jika kita meletakkan selembar logam di antaranya, dan membuat dua celah yang sangat sempit di lembaran tersebut, ketika kita menembakkan banyak foton pada lembaran logam, dan mereka harus melalui celah, maka kita akan melihat sesuatu yang luar biasa. Sepanjang jalan di seluruh lembaran film yang dikembangkan, kita akan melihat serangkaian pita terang dan gelap. Kita bisa menggunakan matematika untuk mengetahui dengan tepat di mana pita terang akan berada dan seberapa terang cahaya yang membuatnya, yaitu, kita bisa mengetahui sebelumnya berapa banyak foton yang akan jatuh pada setiap pita. Tetapi, jika kita memperlambat prosesnya dan melihat di mana setiap foton mendarat di layar, kita tidak akan pernah tahu sebelumnya di mana foton berikutnya akan muncul. Kita dapat mengetahui dengan pasti bahwa kemungkinan besar foton akan mengenai pita terang di tengah, dan semakin kecil kemungkinan foton akan muncul pada pita yang semakin jauh dari pusat. Jadi kita tahu pasti bahwa pita-pita itu akan paling terang di pusat dan semakin lama semakin redup. Tetapi kita tidak pernah tahu pasti foton mana yang akan masuk ke pita yang mana.
Salah satu kesimpulan aneh dari teori QM adalah efek "kucing Schrödinger". Sifat-sifat tertentu dari sebuah partikel, seperti posisi, kecepatan gerak, arah gerak, dan "spin", tidak dapat dibicarakan sampai ada sesuatu yang mengukurnya (foton yang memantul dari elektron akan dihitung sebagai pengukuran posisinya, misalnya). Sebelum pengukuran, partikel berada dalam "superposisi keadaan", di mana sifat-sifatnya memiliki banyak nilai pada saat yang sama. Schrödinger mengatakan bahwa mekanika kuantum seakan-akan mengatakan bahwa jika sesuatu (seperti hidup atau matinya seekor kucing) ditentukan oleh suatu peristiwa kuantum, maka keadaannya akan ditentukan oleh keadaan yang dihasilkan dari peristiwa kuantum, tetapi hanya pada saat seseorang melihat keadaan peristiwa kuantum tersebut. Pada saat sebelum keadaan peristiwa kuantum itu dilihat, mungkin "kucing yang hidup dan mati (maafkan ungkapannya) [tercampur atau tercecer dalam bagian yang sama."
Konstanta Planck yang dikurangi
Orang sering menggunakan simbol ℏ {\displaystyle \hbar } 

Contoh
Partikel dalam sumur 1 dimensi adalah contoh paling sederhana yang menunjukkan bahwa energi partikel hanya dapat memiliki nilai tertentu. Energi dikatakan "terkuantisasi". Sumur memiliki energi potensial nol di dalam suatu rentang dan memiliki energi potensial tak terbatas di mana-mana di luar rentang itu. Untuk kasus 1-dimensi dalam arah x {\displaystyle x}
- ℏ 2 2 m d 2 ψ d x 2 = E ψ . {\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}=E\psi . }
Dengan menggunakan persamaan diferensial, kita dapat melihat bahwa ψ {\displaystyle \psi }
atau
ψ = C sin k x + D cos k x {\displaystyle \psi =C\sin kx+D\cos kx\; }
Dinding-dinding kotak berarti bahwa fungsi gelombang harus memiliki bentuk khusus. Fungsi gelombang partikel harus nol kapan saja dinding-dindingnya tak terhingga tingginya. Pada setiap dinding:
ψ = 0 a t x = 0 , x = L {\displaystyle \psi =0\;\mathrm {at} \;\;x=0,\;x=L}
Pertimbangkan x = 0
- sin 0 = 0, cos 0 = 1. Untuk memenuhi ψ = 0 {\displaystyle \scriptstyle \psi =0\; }
suku cos harus dihilangkan. Oleh karenanya D = 0
Sekarang perhatikan: ψ = C sin k x {\displaystyle \scriptstyle \psi =C\sin kx\; }
- pada x = L, ψ = C sin k L = 0 {\displaystyle \scriptstyle \psi =C\sin kL=0\; }
- Jika C = 0 maka ψ = 0 {\displaystyle \scriptstyle \psi =0\; }
untuk semua x. Solusi ini tidak berguna.
- oleh karena itu sin kL = 0 harus benar, memberikan kita
k L = n π n = 1 , 2 , 3 , 4 , 5 , ... . {\displaystyle kL=n\pi \;\;\;\;\;n=1,2,3,4,5,...\; }
Kita dapat melihat bahwa n {\displaystyle n}
Halaman terkait
- Gelombang elektromagnetik
- Elektron
- Foton
- Keterikatan kuantum
- Persamaan Schrödinger
Pertanyaan dan Jawaban
T: Apa itu mekanika kuantum?
J: Mekanika kuantum adalah cabang fisika yang menjelaskan bagaimana alam semesta bekerja pada skala yang lebih kecil dari atom. Ia juga dikenal sebagai fisika kuantum atau teori kuantum.
T: Apa arti istilah "kuantum"?
J: Istilah "kuantum" berasal dari bahasa Latin dan berarti "seberapa banyak". Kuantum energi adalah jumlah paling sedikit yang mungkin (atau jumlah ekstra paling sedikit), dan mekanika kuantum menjelaskan bagaimana energi itu bergerak atau berinteraksi.
T: Apa itu partikel subatomik?
J: Partikel subatomik adalah partikel yang membentuk atom, seperti proton, neutron, dan elektron. Partikel-partikel ini bahkan lebih kecil daripada atom.
T: Bagaimana mekanika kuantum menjelaskan bagaimana partikel-partikel ini bekerja?
J: Mekanika kuantum memberikan aturan matematis untuk mempelajari partikel subatomik dan gelombang elektromagnetik untuk memahami perilaku dan interaksi mereka satu sama lain.
T: Apa itu dualitas gelombang-partikel?
J: Dualitas gelombang-partikel mengacu pada fakta bahwa partikel dan gelombang dapat berperilaku seperti satu sama lain - mereka bukan dua entitas yang berbeda, melainkan sesuatu seperti keduanya digabungkan menjadi satu fenomena.
T: Bagaimana fisika modern dapat dijelaskan dengan menggunakan mekanika kuantum?
J: Fisika dan kimia modern dapat dijelaskan dengan menerapkan aturan matematis mekanika kuantum padanya.
Cari di dalam ensiklopedia







