Aljabar

Sejarah

Bentuk-bentuk awal aljabar dikembangkan oleh orang-orang Babilonia dan para ahli geometri Yunani seperti Hero dari Alexandria. Namun kata "aljabar" adalah bentuk Latin dari kata Arab Al-Jabr ("pengecoran") dan berasal dari buku matematika Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah, ("Esai tentang Komputasi Pengecoran dan Persamaan") yang ditulis pada abad ke-9 oleh seorang matematikawan Persia, Muhammad bin Mūsā al-Khwārizmī, yang adalah seorang Muslim yang lahir di Khwarizm di Uzbekistan. Dia berkembang di bawah Al-Ma'moun di Baghdad, Irak sepanjang 813-833 M, dan meninggal sekitar tahun 840 M. Buku ini dibawa ke Eropa dan diterjemahkan ke dalam bahasa Latin pada abad ke-12. Buku itu kemudian diberi nama 'Aljabar'. (Akhiran nama matematikawan, al-Khwarizmi, diubah menjadi kata yang lebih mudah diucapkan dalam bahasa Latin, dan menjadi kata algorithm dalam bahasa Inggris).

Contoh

Berikut ini adalah contoh sederhana dari masalah aljabar:

Sue memiliki 12 permen, dan Ann memiliki 24 permen. Mereka memutuskan untuk berbagi sehingga mereka memiliki jumlah permen yang sama. Berapa banyak permen yang akan dimiliki masing-masing?

Berikut ini adalah langkah-langkah yang bisa Anda gunakan untuk menyelesaikan masalah:

1. Untuk memiliki jumlah permen yang sama, Ann harus memberikan beberapa permen kepada Sue. Misalkan x menyatakan banyaknya permen yang diberikan Ann kepada Sue.
2. Permen Sue, ditambah x, harus sama dengan permen Ann dikurangi x. Hal ini ditulis sebagai: 12 + x = 24 - x
3. Kurangi 12 dari kedua sisi persamaan. Ini memberikan: x = 12 - x. (Apa yang terjadi di satu sisi tanda sama dengan harus terjadi di sisi lain juga, agar persamaan tersebut tetap benar. Jadi dalam kasus ini ketika 12 dikurangi dari kedua sisi, ada langkah tengah 12 + x - 12 = 24 - x - 12. Setelah seseorang merasa nyaman dengan ini, langkah tengah tidak dituliskan).
4. Tambahkan x ke kedua sisi persamaan. Ini menghasilkan: 2x = 12
5. Bagilah kedua sisi persamaan dengan 2. Ini memberikan x = 6. Jawabannya adalah enam. Jika Ann memberikan Sue 6 permen, mereka akan memiliki jumlah permen yang sama.
6. Untuk mengecek ini, masukkan kembali 6 ke dalam persamaan asli di mana pun x berada: 12 + 6 = 24 - 6
7. Ini memberikan 18=18, yang benar. Mereka masing-masing sekarang memiliki 18 permen.

Dengan latihan, aljabar dapat digunakan ketika dihadapkan dengan masalah yang terlalu sulit untuk dipecahkan dengan cara lain. Masalah seperti membangun jalan bebas hambatan, mendesain telepon seluler, atau menemukan obat untuk suatu penyakit, semuanya membutuhkan aljabar.

Menulis aljabar

Seperti di sebagian besar bagian matematika, menambahkan z ke y (atau y plus z) ditulis sebagai y + z. Mengurangkan z dari y (atau y minus z) ditulis sebagai y - z. Membagi y dengan z (atau y lebih dari z: y z {\displaystyle y \over z} ) ditulis sebagai y ÷ z atau y/z. y/z lebih umum digunakan.

Dalam aljabar, mengalikan y dengan z (atau y dikalikan z) dapat ditulis dalam 4 cara: y × z, y * z, y-z, atau hanya yz. Simbol perkalian "×" biasanya tidak digunakan, karena terlalu mirip dengan huruf x, yang sering digunakan sebagai variabel. Juga, ketika mengalikan ekspresi yang lebih besar, tanda kurung dapat digunakan: y (z+1).

Ketika kita mengalikan angka dan huruf dalam aljabar, kita menulis angka di depan huruf: 5 × y = 5y. Ketika angkanya adalah 1, maka 1 tidak ditulis karena 1 dikalikan angka apa pun adalah angka itu (1 × y = y) sehingga tidak diperlukan.

Sebagai catatan tambahan, Anda tidak harus menggunakan huruf x atau y dalam aljabar. Variabel hanyalah simbol yang berarti beberapa angka atau nilai yang tidak diketahui, sehingga Anda dapat menggunakan variabel apa pun. x dan y adalah yang paling umum.

Fungsi dan Grafik

Bagian penting dari aljabar adalah studi tentang fungsi, karena fungsi sering muncul dalam persamaan yang kita coba selesaikan. Fungsi itu seperti mesin yang bisa Anda masukkan angka (atau angka-angka) ke dalamnya dan mengeluarkan angka (atau angka-angka) tertentu. Ketika menggunakan fungsi, grafik bisa menjadi alat yang ampuh dalam membantu kita mempelajari solusi persamaan.

Grafik adalah gambar yang menunjukkan semua nilai variabel yang membuat persamaan atau pertidaksamaan menjadi benar. Biasanya ini mudah dibuat bila hanya ada satu atau dua variabel. Grafik sering kali berupa garis, dan jika garis tidak melengkung atau lurus ke atas dan ke bawah, maka dapat digambarkan dengan rumus dasar y = mx + b. Variabel b adalah intersep y dari grafik (di mana garis melintasi sumbu vertikal) dan m adalah kemiringan atau kecuraman garis. Rumus ini berlaku untuk koordinat grafik, dimana setiap titik pada garis ditulis (x, y).

Dalam beberapa soal matematika seperti persamaan garis, mungkin ada lebih dari satu variabel (x dan y dalam kasus ini). Untuk menemukan titik-titik pada garis, satu variabel diubah. Variabel yang diubah disebut variabel "independen". Kemudian matematika dilakukan untuk membuat angka. Angka yang dibuat disebut variabel "dependen". Sering kali variabel independen ditulis sebagai x dan variabel dependen ditulis sebagai y, misalnya, dalam y = 3x + 1. Ini sering diletakkan pada grafik, misalnya, dalam y = 3x + 1. Hal ini sering diletakkan pada grafik, dengan menggunakan sumbu x (ke kiri dan ke kanan) dan sumbu y (ke atas dan ke bawah). Ini juga bisa ditulis dalam bentuk fungsi: f(x) = 3x + 1. Jadi dalam contoh ini, kita bisa memasukkan 5 untuk x dan mendapatkan y = 16. Masukkan 2 untuk x akan mendapatkan y = 7. Dan 0 untuk x akan mendapatkan y = 1. Jadi akan ada garis yang melalui titik-titik (5,16), (2,7), dan (0,1) seperti yang terlihat pada grafik di sebelah kanan.

Jika x memiliki pangkat 1, itu adalah garis lurus. Jika kuadrat atau pangkat lainnya, maka akan melengkung. Jika menggunakan pertidaksamaan (< atau > ), maka biasanya bagian dari grafik diarsir, baik di atas atau di bawah garis.

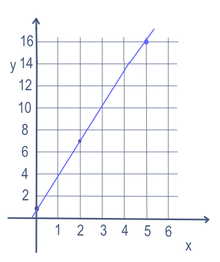
Persamaan linear untuk y=3x+1

Aturan aljabar

Dalam aljabar, ada beberapa aturan yang dapat digunakan untuk pemahaman lebih lanjut tentang persamaan. Ini disebut aturan aljabar. Meskipun aturan-aturan ini mungkin tampak tidak masuk akal atau jelas, adalah bijaksana untuk memahami bahwa sifat-sifat ini tidak berlaku di semua cabang matematika. Oleh karena itu, akan berguna untuk mengetahui bagaimana aturan aksiomatik ini dinyatakan, sebelum menerima begitu saja. Sebelum melanjutkan ke aturan-aturannya, renungkanlah dua definisi yang akan diberikan.

1. Opposite - kebalikan dari {\displaystyle a} adalah - a {\displaystyle -a} .
2. Reciprocal - reciprocal dari {\displaystyle a} adalah 1 a {\displaystyle {\frac {1}{a}}} .

Aturan

Sifat komutatif dari penjumlahan

'Komutatif' berarti bahwa suatu fungsi memiliki hasil yang sama jika angka-angkanya ditukar. Dengan kata lain, urutan suku-suku dalam persamaan tidak menjadi masalah. Ketika operator dari dua suku adalah penjumlahan, 'sifat komutatif penjumlahan' berlaku. Dalam istilah aljabar, ini memberikan a + b = b + a {\displaystyle a+b=b+a} .

Perhatikan bahwa ini tidak berlaku untuk pengurangan! (yaitu, a - b ≠ b - a {\displaystyle a-b\neq b-a} )

Sifat komutatif dari perkalian

Ketika operator dari dua suku adalah perkalian, 'sifat komutatif perkalian' berlaku. Dalam istilah aljabar, ini memberikan a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} .

Perhatikan bahwa ini tidak berlaku untuk pembagian! (yaitu, a b ≠ b a {\displaystyle {\frac {a}{b}}}\neq {\frac {b}{{a}}}}) , ketika a ≠ b {\displaystyle a\neq b} )

Sifat asosiatif dari penjumlahan

'Asosiatif' mengacu pada pengelompokan angka. Sifat asosiatif dari penjumlahan menyiratkan bahwa, ketika menambahkan tiga suku atau lebih, tidak masalah bagaimana suku-suku ini dikelompokkan. Secara aljabar, hal ini memberikan a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} . Perhatikan bahwa hal ini tidak berlaku untuk pengurangan, misalnya 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\displaystyle 1 = 0 - ( 0 - 1 ) = (0 - 1 )\neq (0 - 0 )-1 = - 1} (lihat properti distributif).

Sifat asosiatif perkalian

Sifat asosiatif perkalian menyiratkan bahwa, ketika mengalikan tiga suku atau lebih, tidak masalah bagaimana suku-suku ini dikelompokkan. Secara aljabar, ini memberikan a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c} . Perhatikan bahwa hal ini tidak berlaku untuk pembagian, misalnya 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\displaystyle 2 = 1 / ( 1/2 ) \neq (1 / 1 ) / 2 = 1 / 2} .

Properti distributif

Sifat distributif menyatakan bahwa perkalian suatu bilangan dengan suku lain dapat didistribusikan. Sebagai contoh: a ⋅ ( b + c ) = a b + a c {\displaystyle a\cdot (b+c)=ab+ac} . (Jangan bingung dengan sifat asosiatif! Misalnya, a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\displaystyle a\cdot (b+c)\neq (a\cdot b)+c} .)

Properti identitas aditif

'Identitas' mengacu pada sifat suatu bilangan yang sama dengan dirinya sendiri. Dengan kata lain, ada operasi dua bilangan sehingga sama dengan variabel dari jumlah tersebut. Sifat identitas aditif menyatakan bahwa jumlah dari sembarang bilangan dan 0 adalah bilangan itu: a + 0 = a {\displaystyle a+0=a} . Ini juga berlaku untuk pengurangan: a - 0 = a {\displaystyle a-0=a} .

Properti identitas multiplikatif

Sifat identitas multiplikatif menyatakan bahwa hasil perkalian bilangan apapun dan 1 adalah bilangan itu: a ⋅ 1 = a {\displaystyle a\cdot 1=a} . Ini juga berlaku untuk pembagian: a 1 = a {\displaystyle {\frac {a}{1}}=a} .

Properti inversi aditif

Sifat invers aditif agak mirip dengan kebalikan dari sifat identitas aditif. Ketika suatu operasi adalah jumlah dari suatu bilangan dan kebalikannya, dan itu sama dengan 0, operasi itu adalah operasi aljabar yang valid. Secara aljabar, dinyatakan sebagai berikut: a - a = 0 {\displaystyle a-a=0} . Invers aditif dari 1 adalah (-1).

Properti invers multiplikatif

Sifat invers multiplikatif mensyaratkan bahwa ketika suatu operasi adalah hasil kali dari suatu bilangan dan kebalikannya, dan itu sama dengan 1, operasi itu adalah operasi aljabar yang valid. Secara aljabar, sifat ini menyatakan sebagai berikut: a a = 1 {\displaystyle {\frac {a}{a}}}=1} . Invers multiplikatif dari 2 adalah 1/2.

Aljabar Lanjutan

Selain "aljabar dasar", atau aljabar dasar, ada bentuk aljabar tingkat lanjut, yang diajarkan di perguruan tinggi dan universitas, seperti aljabar abstrak, aljabar linear, dan aljabar universal. Ini termasuk cara menggunakan matriks untuk menyelesaikan banyak persamaan linear sekaligus. Aljabar abstrak adalah studi tentang hal-hal yang ditemukan dalam persamaan, melampaui angka-angka ke yang lebih abstrak dengan kelompok angka.

Banyak soal matematika yang berkaitan dengan fisika dan teknik. Dalam banyak masalah fisika ini waktu adalah variabel. Waktu menggunakan huruf t. Menggunakan ide-ide dasar dalam aljabar dapat membantu mengurangi masalah matematika ke bentuk yang paling sederhana sehingga lebih mudah untuk memecahkan masalah yang sulit. Energi adalah e, gaya adalah f, massa adalah m, akselerasi adalah a dan kecepatan cahaya kadang-kadang c. Ini digunakan dalam beberapa persamaan terkenal, seperti f = ma dan e = mc ^ 2 (meskipun matematika yang lebih kompleks di luar aljabar diperlukan untuk menghasilkan persamaan terakhir itu).

Halaman terkait

• Daftar topik matematika
• Urutan Operasi
• Parabola
• Sistem Aljabar Komputer