Ketidaksetaraan
Ketidaksetaraan adalah ketika satu objek:
- lebih kecil dari yang lain ( a < b {\displaystyle \ a<b}
berarti a lebih kecil dari b)
- lebih besar dari yang lain ( a > b {\displaystyle \ a>b}
berarti a lebih besar dari b)
- tidak lebih kecil dari yang lain ( a ≥ b {\displaystyle a\geq b}
berarti a tidak lebih kecil dari b, yaitu lebih besar, atau sama dengan b)
- tidak lebih besar dari yang lain ( a ≤ b {\displaystyle a\leq b}
berarti a tidak lebih besar dari b, atau lebih kecil atau sama dengan b)
Ketidaksamaan kadang-kadang digunakan untuk menamai pernyataan bahwa satu ekspresi lebih kecil, lebih besar, tidak lebih kecil atau tidak lebih besar dari yang lain.
Bekerja dengan ketidaksetaraan
Ketidaksamaan dalam matematika adalah ketika dua solusi atau jawaban dibandingkan dengan lebih besar dari atau kurang dari. Ini adalah ketika dua atau banyak solusi yang dibandingkan tidak memiliki jumlah yang sama. Memecahkan pertidaksamaan berarti menemukan solusinya. Ketika Anda mensubstitusikan angka ke variabel dan pernyataannya benar, maka itu adalah solusi. Ketika Anda mensubstitusikan angka ke variabel dan pernyataannya tidak benar, maka angka tersebut bukan solusi untuk pernyataan tersebut.
Ketidaksetaraan adalah menemukan solusi untuk variabel yang diberikan. Ini adalah menemukan urutan relatif dari suatu himpunan. Pertidaksamaan memiliki banyak solusi tetapi Anda perlu menemukan solusi nyata. Pertidaksamaan adalah menyelesaikan bilangan real. Cara yang tepat untuk membaca pertidaksamaan adalah dari kiri ke kanan, sama seperti persamaan lainnya, tetapi satu-satunya perbedaan adalah mereka memiliki aturan yang berbeda untuk setiap persamaan.
Misalnya, x+4>12, di mana x adalah bilangan real. Pertama, seseorang perlu menemukan x dan dia perlu tahu apakah itu adalah solusi. Jawabannya adalah x>8 dan itu adalah pernyataan yang benar. Ungkapan ini adalah tentang lokasi x dalam himpunan bilangan real. Garis bilangan adalah salah satu cara untuk menunjukkan lokasi relatif terhadap semua bilangan real lainnya. (Lihat gambar Ketidaksamaan 1)
.jpg)
Pertidaksamaan 1 Ini adalah solusi untuk persamaan x+4>12
Berbagai jenis ketidaksetaraan
Ada lima jenis ketidaksetaraan yang berbeda:
- Yang pertama adalah pertidaksamaan linear yang merupakan pertidaksamaan yang membedakan ekspresi dengan kurang dari atau sama dengan, kurang dari atau lebih besar dari atau sama dengan, lebih besar dari. Ini adalah salah satu yang jika kita mengganti pertidaksamaan untuk hubungan sama dengan, maka hasilnya akan menjadi persamaan linier.
- Yang kedua adalah kombinasi dari pertidaksamaan yang mana untuk memenuhi pertidaksamaan, Anda harus memiliki angka dalam himpunan solusi sehingga angka-angka yang memenuhi pertidaksamaan akan menjadi nilai dalam persilangan dari dua himpunan solusi.
- Yang ketiga adalah pertidaksamaan yang melibatkan nilai absolut yang berarti bahwa nilai-nilai tersebut dapat diulang sebagai kombinasi dari pertidaksamaan yang akan melibatkan nilai absolut.
- Yang keempat disebut pertidaksamaan polinomial yang berarti kontinu, artinya grafiknya tidak memiliki lompatan atau jeda.
- Terakhir, adalah pertidaksamaan rasional, yang berarti bahwa itu adalah bentuk salah satu polinomial dibagi dengan polinomial. Dengan kata lain, grafik fungsi rasional tidak memiliki jeda atau mewakili pada nol dari penyebutnya.
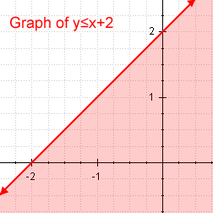
Ketidaksamaan Linear Contoh ketidaksamaan linear
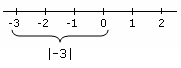
nilai absolut Contoh yang menunjukkan nilai absolut
Empat cara untuk menyelesaikan Ketidaksetaraan
Ada empat cara untuk menyelesaikan persamaan kuadrat:
- Aturan nomor satu adalah Anda harus menambahkan atau mengurangi angka yang sama di kedua sisi.
- Aturan nomor dua adalah Anda harus menggeser sisi-sisinya dan mengubah posisi tanda pertidaksamaan.
- Aturan nomor tiga adalah Anda harus memperbanyak.
- Aturan nomor empat adalah membagi bilangan positif atau negatif yang sama ke dalam kedua sisi. Tetapi, Anda hanya dapat menggunakan ini pada soal pertidaksamaan yang mudah.
Selanjutnya, dibutuhkan dua langkah untuk menyelesaikan pertidaksamaan. Yang pertama adalah menyederhanakan dengan menggunakan kebalikan dari penjumlahan atau pengurangan. Yang kedua adalah menyederhanakan lebih banyak dengan menggunakan kebalikan dari perkalian atau pembagian. Saat Anda mengalikan atau membagi pertidaksamaan dengan bilangan negatif, ingatlah untuk mengubah simbol pertidaksamaan.

Contoh penambahan ketidaksetaraan.

contoh perkalian Ketidaksetaraan
Contoh-contoh cara menyelesaikan Pertidaksamaan
Pertidaksamaan adalah pernyataan matematika yang menjelaskan bahwa dua nilai tidak sama dan berbeda. Persamaan ab berarti a tidak sama dengan b. Pertidaksamaan sama dengan persamaan apa pun tetapi satu-satunya perbedaan adalah bahwa pertidaksamaan tidak menggunakan tanda sama dengan menggunakan simbol. Pertidaksamaan b>a menunjukkan bahwa b lebih besar dari a. Batas kecepatan, tanda, dan lainnya menggunakan pertidaksamaan untuk menyatakannya.
Saat menyelesaikan pertidaksamaan, seseorang harus memiliki pernyataan yang benar. Ketika Anda membagi atau mengalikan pertidaksamaan dengan angka negatif di kedua sisi, pernyataan itu salah, untuk membuat pernyataan yang benar dengan angka negatif, Anda perlu membalik simbol untuk membuat pernyataan itu benar. Ketika suatu bilangan adalah bilangan positif, Anda tidak perlu membalik simbolnya. Ketidaksetaraan adalah tentang membuat pernyataan yang benar.
Sebagai contoh, mulailah dengan pernyataan benar -6y<-12. Ketika kedua sisi dibagi dengan -6 hasilnya akan menjadi y<2. Dalam pernyataan ini simbol perlu dibalik agar memiliki pernyataan yang benar, y>2 adalah jawaban yang benar. Pada garis bilangan (lihat gambar Pertidaksamaan 2), lingkaran yang diarsir tertutup menunjukkan bahwa itu termasuk dalam himpunan penyelesaian. Lingkaran terbuka menunjukkan bahwa itu tidak termasuk dalam himpunan penyelesaian.
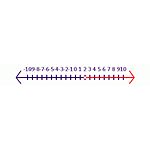
Pertidaksamaan 2 Solusi untuk persamaan -6y<-12
Halaman terkait
- Kesetaraan (matematika)
- Persamaan
Pertanyaan dan Jawaban
T: Apa arti dari "a < b"?
J: Artinya a lebih kecil dari b.
T: Apa artinya "a > b"?
J: Artinya a lebih besar dari b.
T: Apa artinya "a ≥ b"?
J: Artinya a tidak lebih kecil dari b, yaitu lebih besar atau sama dengan b.
T: Apa arti dari "a ≤ b"?
J: Artinya a tidak lebih besar dari b, atau lebih kecil atau sama dengan b.
T: Bagaimana pertidaksamaan dapat digunakan dalam matematika?
A: Pertidaksamaan dapat digunakan untuk menamai pernyataan bahwa satu ekspresi lebih kecil, lebih besar, tidak lebih kecil atau tidak lebih besar dari yang lain.
Cari di dalam ensiklopedia