Fungsi (matematika)
Dalam matematika, fungsi adalah objek matematika yang menghasilkan output, ketika diberi input - bisa berupa angka, vektor, atau apa pun yang bisa ada di dalam sekumpulan hal.
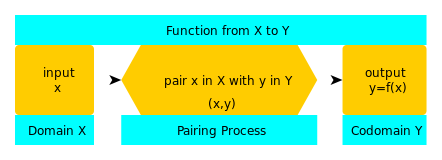
Jadi, fungsi itu seperti mesin, yang mengambil nilai x dan mengembalikan output y. Himpunan semua nilai yang dapat dimiliki x disebut domain. Himpunan yang berisi setiap nilai yang dapat dimiliki y disebut kodomain.
Jika hal ini terjadi, kita katakan bahwa y adalah fungsi dari x, dan kita tulis y =f(x). f adalah nama fungsi dan kita tulis f : X → Y {\displaystyle f:X\ke Y}
Contoh fungsi adalah f(x)=x+1 Seseorang memberikan bilangan asli x {\displaystyle x}


Metafora
Tabel

Input dan output bisa dimasukkan ke dalam tabel seperti gambar; ini mudah jika datanya tidak terlalu banyak.
Grafik

Pada gambar terlihat bahwa 2 dan 3 telah dipasangkan dengan c; hal ini tidak diperbolehkan pada arah yang lain, 2 tidak bisa mengeluarkan c dan d, setiap input hanya bisa memiliki satu output. Semua f ( x ) {\displaystyle f(x)}


Sejarah
Pada tahun 1690-an Gottfried Leibniz dan Johann Bernoulli menggunakan kata fungsi dalam huruf-huruf di antara mereka sehingga konsep modern dimulai pada saat yang sama dengan kalkulus.
Pada tahun 1748 Leonhard Euler memberikan: "Fungsi dari kuantitas variabel adalah ekspresi analitik yang tersusun dengan cara apa pun dari kuantitas variabel dan angka atau kuantitas konstan." dan kemudian pada tahun 1755: "Jika beberapa kuantitas sangat bergantung pada kuantitas lain sehingga jika kuantitas yang terakhir diubah, kuantitas yang pertama mengalami perubahan, maka kuantitas yang pertama disebut fungsi dari kuantitas yang terakhir. Definisi ini berlaku agak luas dan mencakup semua cara di mana satu kuantitas dapat ditentukan oleh kuantitas lainnya. Jika, oleh karena itu, x menunjukkan kuantitas variabel, maka semua kuantitas yang bergantung pada x dengan cara apa pun, atau ditentukan olehnya, disebut fungsi dari x." yang sangat modern.
Biasanya, Dirichlet dikreditkan dengan versi yang digunakan di sekolah-sekolah sampai paruh kedua abad ke-20: "y adalah fungsi dari variabel x, yang didefinisikan pada interval a < x < b, jika untuk setiap nilai variabel x dalam interval ini terdapat nilai pasti dari variabel y. Juga, tidak relevan dengan cara apa korespondensi ini ditetapkan."
Pada tahun 1939, Bourbaki menggeneralisasi definisi Dirichlet dan memberikan versi teori himpunan dari definisi sebagai korespondensi antara input dan output; ini digunakan di sekolah-sekolah dari sekitar tahun 1960.
Akhirnya pada tahun 1970, Bourbaki memberikan definisi modern sebagai triple f = ( X , Y , F ) {\displaystyle f=(X,Y,F)}



Jenis-jenis fungsi
- Fungsi dasar - Fungsi-fungsi yang biasanya dipelajari di sekolah: pecahan, akar kuadrat, fungsi sinus, kosinus dan tangen, dan beberapa fungsi lainnya.
- Fungsi non-elementer - Kebanyakan dari mereka tidak menggunakan operasi yang tidak kita pelajari di sekolah (seperti + atau -, atau pangkat). Banyak integral yang bukan elementer.
- Fungsi invers - Fungsi yang membatalkan fungsi lain. Contohnya: jika F(x) adalah invers dari f(x)=y, maka F(y)=x. Tidak semua fungsi memiliki invers.
- Fungsi-fungsi khusus: Fungsi yang memiliki nama. Misalnya: sinus, kosinus dan tangen. Fungsi seperti f(x)=3x (tiga kali x) tidak disebut fungsi khusus. Mereka bisa berupa fungsi elementer, non-elementer atau invers.
| Kontrol otoritas |
|
Pertanyaan dan Jawaban
T: Apa yang dimaksud dengan fungsi dalam matematika?
J: Fungsi dalam matematika adalah objek yang menghasilkan output ketika diberi input, yang bisa berupa angka, vektor atau apa pun yang bisa ada di dalam sekumpulan hal.
T: Apa dua himpunan yang terkait dengan fungsi?
J: Himpunan semua nilai yang dapat dimiliki x disebut domain dan himpunan yang berisi setiap nilai yang dapat dimiliki y disebut kodomain.
T: Bagaimana fungsi sering dilambangkan?
J: Fungsi sering dilambangkan dengan huruf miring seperti f, g, h.
T: Bagaimana kita merepresentasikan sebuah fungsi?
J: Kita merepresentasikan sebuah fungsi dengan menulis y = f(x), dimana f adalah nama dari fungsi tersebut dan kita menulis f : X → Y (fungsi dari X ke Y) untuk merepresentasikan tiga bagian dari fungsi - domain (X), kodomain (Y) dan proses pasangan (panah).
T: Dapatkah Anda memberikan contoh dari sebuah fungsi?
J: Contoh fungsi adalah f(x) = x + 1. Seseorang memberikan bilangan asli x sebagai input dan mendapatkan bilangan asli y yang merupakan x + 1. Misalnya, memberikan 3 sebagai input ke f menghasilkan output 4.
T: Apakah setiap fungsi harus berupa persamaan?
J: Tidak, tidak setiap fungsi harus berupa persamaan. Ide utama di balik fungsi adalah bahwa input dan output dipasangkan entah bagaimana caranya - bahkan jika itu mungkin sangat rumit.
Cari di dalam ensiklopedia