Prinsip ketidakpastian

Diagram

1. Foton, elektron, dan partikel sub-atomik lainnya akan menjadi fokus yang tajam ketika ditembakkan melalui lubang besar, tetapi kita tidak tahu persis di mana mereka berada di tengah jalan.


2. Mempersempit lubang akan membengkokkan jalur partikel di sekitar tepi lubang (difraksi) sehingga sinar yang dihasilkan menjadi lebih besar dan lebih lembut.


3. Mempersempit lubang meningkatkan kepastian di mana foton berada di tengah, tetapi kemudian arahnya dari sana ke layar pendeteksian di sebelah kanan menjadi lebih tidak pasti. Fokus menjadi kabur. Memperlebar lubang membuat semua foton berakhir di tengah layar deteksi, tetapi kemudian kita kurang mengetahui di mana foton berada ketika mereka melewati penghalang pusat.


4. Pemasangan pegas pada penghalang dengan lubang kecil membuat partikel masuk melalui lubang, yang mendorong penghalang, meregangkan pegas, dan dengan demikian mengukur momentum. Tetapi karena penghalang yang dipasang pegas bergerak, kita kurang yakin di mana partikel itu berada ketika melewati lubang, dan difraksi juga akan mempengaruhi posisinya pada layar deteksi.


5. Menangguhkan celah tengah dengan skala pegas memungkinkan momentum diukur, tetapi melakukan hal itu secara tidak terduga menggerakkan celah sehingga informasi tentang lokasi setiap foton di tengah akan hilang.


6. Animasi ini menunjukkan salah satu konsekuensi penting dari sifat ketidakpastian alam semesta: terowongan kuantum elektron. Perhatikan baik-baik. Setiap kali ada sedikit yang melewati penghalang.

Bagaimana manusia belajar tentang ketidakpastian?

Tak lama setelah Werner Heisenberg menciptakan fisika kuantum baru, sesuatu yang tak terduga keluar dari matematikanya, yaitu ungkapan:

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {h}{4\pi }}\qquad \qquad \qquad }

Kisaran kesalahan dalam posisi (x) dikalikan kisaran kesalahan dalam momentum (p) kira-kira sama atau lebih besar dari konstanta Planck dibagi 4π.

Simbol-simbol ini dimasukkan ke dalam bentuk matematika, apa yang telah Anda lihat pada gambar-gambar di atas. Simbol-simbol ini mengatakan, dengan cara yang jelas, bahwa Anda tidak bisa benar-benar yakin tentang di mana sesuatu berada dan ke mana arahnya. Jika Anda semakin jelas di mana ia berada pada suatu waktu, maka Anda tidak akan tahu ke mana ia akan pergi dan seberapa cepat. Jika Anda menjadi lebih jelas tentang ke mana ia pergi dan seberapa cepat setiap saat, maka Anda memiliki sedikit gagasan tentang di mana ia berada saat ini.

Para ilmuwan telah mengetahui, mengapa zat-zat tertentu memancarkan warna cahaya yang khas ketika zat-zat tersebut dipanaskan atau tereksitasi. Heisenberg mencoba menjelaskan mengapa warna-warna ini masing-masing memiliki kecerahan yang khas. Tidak akan cukup baik jika dia dan para ilmuwan lainnya hanya berkata, "Yah, begitulah adanya." Mereka yakin bahwa pasti ada alasan yang baik untuk perbedaan-perbedaan ini, dan untuk fakta bahwa rasio di antara kekuatan garis terang selalu sama untuk setiap sampel elemen.

Dia tidak tahu bahwa dia akan tersandung pada rahasia alam yang tersembunyi ketika dia berangkat untuk menemukan penjelasan untuk intensitas karakteristik garis berwarna dari masing-masing elemen. Studi mekanika kuantum telah menunjukkan mengapa hidrogen memiliki empat garis terang di bagian spektrum yang dapat dilihat manusia. Pasti tampak bahwa hal berikutnya yang harus dipelajari adalah bagaimana menghitung kecerahannya. Hidrogen tampaknya menjadi tempat yang jelas untuk memulai karena hidrogen hanya memiliki satu elektron untuk ditangani, dan hanya empat garis di bagian spektrum yang terlihat. Tentunya harus ada alasan yang bagus untuk tidak sama terangnya. Penjelasan untuk kecerahan garis-garis warna yang berbeda dari neon dan unsur-unsur lainnya bisa menunggu.

 

Heisenberg mulai mengerjakan fisika kuantum dengan mengadaptasi persamaan klasik untuk listrik, yang sangat rumit untuk memulainya, sehingga matematika di balik makalahnya pada tahun 1925 sangat sulit untuk diikuti.

Dia mencoba menemukan cara yang tepat untuk menghitung intensitas garis terang dalam spektrum lampu hidrogen. Dia harus menemukan kuantitas terkait yang disebut "amplitudo" dan mengalikan amplitudo dengan amplitudo (atau dengan kata lain dia harus mengkuadratkan amplitudo) untuk mendapatkan intensitas yang diinginkannya. Dia harus mencari cara untuk mengekspresikan amplitudo dengan cara yang memperhitungkan fakta bahwa lampu hidrogen tidak memancar pada semua frekuensi, dan tidak memancar di seluruh rentang frekuensi yang berkelanjutan di bagian spektrum yang dapat dilihat orang. Heisenberg menemukan cara baru yang luar biasa untuk menghitung amplitudo.

Persamaan aneh yang ditemukan Heisenberg dan digunakan untuk melakukan perkalian satu kuantitas kuantum (misalnya, posisi) dengan yang lain (misalnya, momentum) diterbitkan dalam apa yang disebut "makalah 'ajaib' Heisenberg pada Juli 1925."

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n, n - b) = jumlah _{a}^{}}\,A(n, n - a) B(n - a, n - b)}

Matematika di atas terlihat sangat sulit, tetapi matematika yang mengarah ke sana jauh lebih sulit dan sangat sulit untuk dipahami. Ini diberikan di sini hanya untuk menunjukkan seperti apa kelihatannya. Makalah Heisenberg adalah tengara sejarah. Banyak fisikawan yang membaca makalahnya mengatakan bahwa mereka tidak bisa tidak setuju dengan kesimpulannya, tetapi mereka tidak bisa mengikuti penjelasannya tentang bagaimana dia sampai pada kesimpulan itu. Persamaan awal yang digunakan Heisenberg melibatkan deret Fourier, dan melibatkan banyak faktor. Kita akan kembali ke persamaan di atas karena ini adalah semacam resep untuk menulis dan mengalikan matriks.

Persamaan-persamaan baru harus begitu aneh dan tidak biasa karena Heisenberg menggambarkan dunia yang aneh di mana beberapa hal, seperti orbit elektron, tidak perlahan-lahan menjadi lebih besar atau lebih kecil. Jenis perubahan baru melibatkan lompatan dan celah besar di antara lompatan. Elektron hanya dapat melompat di antara orbit tertentu, dan energi yang diperoleh atau hilang dalam perubahan di antara orbit dihasilkan ketika foton dengan energi yang tepat diserap atau foton baru dengan energi yang tepat diproduksi. Jika elektron dalam atom hidrogen paling sering melompat ke bawah (jatuh) di antara dua orbit tertentu, maka lebih banyak foton akan dipancarkan pada tingkat energi itu, dan cahaya yang dihasilkan pada tingkat itu akan menjadi yang paling kuat.

Sulit untuk membuat persamaan yang dibuat untuk spektrum kontinu (apa yang Anda lihat ketika Anda menempatkan cahaya matahari melalui prisma) sesuai dengan spektrum yang hanya memiliki beberapa frekuensi puncak di antara yang tidak ada apa-apa. Hampir semua yang telah dipelajari tentang cahaya dan energi telah dilakukan dengan benda-benda besar seperti lilin atau matahari yang terbakar, dan benda-benda besar itu semuanya menghasilkan spektrum kontinu. Meskipun benda-benda berukuran biasa ini mudah untuk melakukan eksperimen, namun masih butuh waktu lama untuk mengetahui hukum (fisika) yang mengaturnya. Sekarang para fisikawan berurusan dengan benda-benda yang terlalu kecil untuk dilihat, benda-benda yang tidak menghasilkan spektrum kontinu, dan mencoba menemukan cara untuk setidaknya mendapatkan petunjuk dari apa yang sudah mereka ketahui yang akan membantu mereka menemukan hukum dari sumber cahaya yang kecil dan bercelah ini.

Persamaan aslinya berhubungan dengan sejenis benda bergetar yang akan menghasilkan gelombang, sedikit seperti cara buluh dalam organ akan menghasilkan gelombang suara dengan frekuensi karakteristik. Jadi, ada gerakan ke belakang dan ke depan (seperti getarnya buluh) dan ada gelombang yang dipancarkan yang dapat digambarkan sebagai gelombang sinus. Sebagian besar dari apa yang sebelumnya telah diketahui tentang fisika pada tingkat atom berkaitan dengan elektron yang bergerak di sekitar inti. Ketika massa bergerak dalam orbit, ketika berputar di sekitar semacam hub, ia memiliki apa yang disebut "momentum sudut". Momentum sudut adalah cara sesuatu seperti komidi putar akan terus berputar setelah orang berhenti mendorongnya. Matematika yang digunakan untuk perhitungan fase dan momentum sudut itu rumit. Selain itu, Heisenberg tidak menunjukkan semua perhitungannya dalam makalahnya tahun 1925, jadi bahkan ahli matematika yang baik pun mungkin kesulitan mengisi apa yang tidak dia katakan.

Meskipun banyak fisikawan mengatakan bahwa mereka tidak dapat mengetahui berbagai langkah matematika dalam makalah terobosan Heisenberg, satu artikel baru-baru ini yang mencoba menjelaskan bagaimana Heisenberg mendapatkan hasilnya menggunakan dua puluh halaman yang penuh matematika. Bahkan artikel itu tidak mudah dipahami. Matematika dimulai dengan beberapa hal yang sangat sulit dan pada akhirnya akan menghasilkan sesuatu yang relatif sederhana yang ditunjukkan di bagian atas artikel ini. Mendapatkan hasil yang lebih sederhana itu tidak mudah, dan kami tidak akan mencoba menunjukkan proses mendapatkan dari gambaran alam semesta yang sudah ketinggalan zaman ke fisika kuantum yang baru. Kita hanya perlu cukup detail untuk menunjukkan bahwa segera setelah Heisenberg membuat terobosannya, bagian dari cara kerja alam semesta yang belum pernah dilihat siapa pun sebelumnya mulai terlihat.

Heisenberg pasti sangat bersemangat tetapi juga sangat lelah ketika, larut malam, dia akhirnya membuat terobosan dan mulai membuktikan pada dirinya sendiri bahwa itu akan berhasil. Hampir seketika itu juga dia melihat sesuatu yang aneh, sesuatu yang dia pikir adalah masalah kecil yang menjengkelkan yang bisa dia hilangkan. Tetapi ternyata gangguan kecil ini adalah penemuan besar.

Heisenberg telah bekerja untuk mengalikan amplitudo dengan amplitudo, dan sekarang Heisenberg memiliki cara yang baik untuk mengekspresikan amplitudo menggunakan persamaan barunya. Tentu saja dia berpikir tentang perkalian, dan tentang bagaimana dia akan mengalikan hal-hal yang diberikan dalam hal persamaan yang rumit.

Heisenberg menyadari bahwa selain mengkuadratkan amplitudo, dia pada akhirnya ingin mengalikan posisi dengan momentum, atau mengalikan energi dengan waktu, dan sepertinya akan ada bedanya jika dia mengubah urutan dalam kasus-kasus baru ini. Heisenberg tidak berpikir itu tidak masalah jika seseorang mengalikan posisi dengan momentum atau jika seseorang mengalikan momentum dengan posisi. Jika mereka hanya angka-angka sederhana, tidak akan ada masalah. Tetapi keduanya adalah persamaan yang rumit, dan bagaimana Anda mendapatkan angka-angka untuk dimasukkan ke dalam persamaan ternyata berbeda tergantung pada cara mana Anda memulai. Di alam, Anda harus mengukur posisi dan kemudian mengukur momentum, atau Anda harus mengukur momentum dan kemudian mengukur posisi, dan dalam matematika situasi umum yang sama berlaku. (Lihat artikel Wikipedia bahasa Inggris Heisenberg's entryway to matrix mechanics jika Anda ingin mempelajari detail yang rewel!) Perbedaan kecil tapi sial antara hasil akan tetap ada, tidak peduli seberapa besar Heisenberg berharap mereka akan pergi.

Pada saat itu, Heisenberg tidak dapat menyingkirkan satu masalah kecil itu, tetapi dia kelelahan, jadi dia menyerahkan pekerjaannya kepada atasan langsungnya, Max Born, dan pergi berlibur.

Max Born adalah seorang matematikawan luar biasa yang segera melihat bahwa persamaan yang diberikan Heisenberg kepadanya adalah semacam resep untuk menulis matriks. Born adalah salah satu dari sedikit orang pada waktu itu yang tertarik pada jenis matematika aneh yang kebanyakan orang pikir tidak baik untuk banyak hal. Dia tahu bahwa matriks dapat dikalikan, sehingga melakukan semua perhitungan untuk menghitung satu masalah fisika dapat ditangani dengan mengalikan satu matriks dengan matriks lainnya. Hanya dengan mampu menempatkan prosedur yang rumit ke dalam bentuk standar dan dapat diterima akan membuatnya lebih mudah untuk dikerjakan. Mungkin juga membuatnya lebih mudah diterima oleh orang lain.

Born adalah seorang matematikawan yang baik sehingga dia segera menyadari bahwa mengganti urutan perkalian dua matriks akan menghasilkan hasil yang berbeda, dan hasilnya akan berbeda dalam jumlah yang kecil. Jumlah itu adalah h/2πi. Dalam kehidupan sehari-hari, perbedaan itu akan sangat kecil sehingga kita bahkan tidak bisa melihatnya.

Apabila molekul-molekul tertentu tereksitasi, mereka mengeluarkan warna yang khas.


Spektrum hidrogen


Spektrum neon


Spektrum visual penuh dari matahari. Tidak ada celah. Grafik ini menunjukkan intensitas pada berbagai frekuensi.


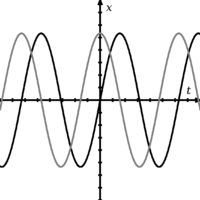
Dua gelombang yang berada di luar fase satu sama lain

Menuju teori formal ketidakpastian

Butuh beberapa tahun, tetapi Heisenberg mampu membuktikan Prinsip Ketidakpastian, yang mengatakan bahwa Δx × Δp = h/2, yang merupakan angka yang keluar dari persamaan asli tetapi meninggalkan π dan i yang berkaitan dengan perubahan fase. Heisenberg menjelaskan bahwa ia menurunkan prinsip ketidakpastiannya dari hasil sebelumnya ini ketika ia menulis makalah pada tahun 1927 yang memperkenalkan teori ini.

Konstanta yang ditulis h, yang disebut konstanta Planck, adalah angka misterius yang sering terjadi, jadi kita perlu memahami apa angka kecil ini. Secara numerik, biasanya diberikan sebagai 6,62607×10^-34 J s (joule detik). Jadi ini adalah kuantitas yang melibatkan energi dan waktu.

Hal ini ditemukan ketika Planck menyadari bahwa energi radiator yang sempurna (disebut radiator benda hitam) dipancarkan dalam satuan ukuran tertentu yang disebut "kuanta" (bentuk tunggal dari kata ini adalah "kuantum"). Energi yang dipancarkan dipancarkan sebagai foton, dan frekuensi foton sebanding dengan "pukulan" yang diberikannya. Kita mengalami frekuensi cahaya tampak yang berbeda sebagai warna yang berbeda. Pada ujung ungu spektrum, setiap foton memiliki jumlah energi yang relatif besar; pada ujung merah spektrum, setiap foton memiliki jumlah energi yang relatif kecil. Cara untuk menghitung jumlah energi foton diberikan oleh persamaan E = hν (energi sama dengan konstanta Planck kali "nu" atau frekuensi).

Prinsip ketidakpastian Heisenberg Δx × Δp ≥ h memberi tahu kita bahwa setiap kali kita mencoba untuk menjabarkan pasangan angka tertentu, kita hanya bisa sedekat itu, dan bahwa jika kita mencoba untuk lebih jelas pada salah satunya, yaitu, jika kita mencoba membuat Δx lebih kecil sehingga kita memiliki gagasan yang lebih baik tentang posisi sesuatu, maka kita harus mendapatkan kembali angka yang lebih besar untuk nomor lain dari pasangan tersebut, dan bahwa jumlah keduanya tidak aktif sangat erat kaitannya dengan h.

Pasangan besaran fisika lainnya berjalan sesuai dengan hubungan ketidakpastian: ΔE × Δt ≥ h, dan pasangan itu menunjukkan, antara lain, bahwa jika kita melihat di ruang antarbintang, beberapa tempat di mana kita tidak berharap menemukan apa pun sama sekali, dan kita mengurangi Δt semakin dekat dan semakin dekat ke 0, maka untuk menjaga keseimbangan yang ditunjukkan dalam persamaan ΔE harus menjadi semakin besar - dan tiba-tiba sesuatu dengan momentum dapat muncul ke dalam eksistensi hanya untuk periode waktu yang singkat itu.

Bagaimana ketidakpastian (kurangnya kepastian) ini bisa dijelaskan? Apa yang sedang terjadi di alam semesta? Sering dikatakan bahwa teori baru yang berhasil dapat memberikan informasi baru tentang fenomena yang sedang diselidiki. Heisenberg menciptakan model matematika yang meramalkan intensitas yang benar untuk spektrum garis terang hidrogen, tetapi tanpa bermaksud melakukannya, ia menemukan bahwa pasangan kuantitas fisik tertentu mengungkapkan ketidakpastian yang tak terduga. Sampai saat itu, tidak ada seorang pun yang tahu bahwa pengukuran tidak bisa selamanya dibuat lebih dan lebih tepat dan akurat. Kenyataan bahwa pengukuran-pengukuran itu tidak dapat dibuat lebih pasti, lebih pasti, merupakan penemuan baru yang menakjubkan. Banyak orang tidak mau menerimanya.

Bohr dan rekan-rekannya berpendapat bahwa foton, elektron, dll. tidak memiliki posisi atau momentum sampai mereka diukur. Posisi teoritis ini tumbuh dari penemuan ketidakpastian, dan bukan hanya beberapa preferensi pribadi tentang apa yang harus dipercaya. Bohr mengatakan bahwa kita tidak tahu apa-apa tentang sesuatu seperti foton atau elektron sampai kita mengamatinya. Untuk mengamati benda sekecil itu, kita perlu berinteraksi dengannya. Dalam kehidupan sehari-hari, kita dapat melakukan sesuatu seperti berjalan di samping mobil sambil menandai waktu mobil itu melintasi titik-titik pada kisi-kisi yang digambar di trotoar. Mungkin berat mobil itu sendiri akan menekan tuas-tuas kecil di trotoar yang akan mematikan jam yang melekat pada masing-masing tuas dan mencatat berat mobil. Pada akhirnya kita akan memiliki catatan yang jelas tentang di mana mobil itu berada pada berbagai waktu, dan juga bisa menghitung arah kemajuan dan beratnya. Kita kemudian bisa mengetahui, kapan saja pada jam tersebut, baik posisi dan momentumnya (kecepatannya dikalikan dengan massanya). Kita bahkan tidak akan membayangkan bahwa gaya yang diperlukan untuk menggerakkan tuas-tuas kecil akan memiliki pengaruh pada kemajuan mobil. Kita juga tidak akan membayangkan bahwa mobil tidak memiliki lokasi atau lintasan di antara titik-titik di trotoar di mana ada tuas, atau bahwa mobil itu ada dalam semacam kekaburan tiga dimensi selama waktu-waktu itu dan hanya menetap ketika sedang menekan tuas. Dunia yang kita kenal tidak mengungkapkan jenis interaksi yang aneh ini.

Untuk menemukan sebuah kapal di laut pada malam hari yang paling gelap, kita bisa menggunakan lampu sorot, dan cahaya itu tidak akan mengganggu posisi atau arah perjalanan kapal, tetapi menemukan elektron dengan cahaya akan memerlukan penembakan dengan satu atau lebih foton yang masing-masing memiliki momentum yang cukup untuk mengganggu posisi dan lintasan elektron. Menemukan elektron dengan cara lain akan melibatkan menahannya dalam semacam pengekangan fisik yang juga akan menghentikan gerakannya ke depan.

Untuk menemukan foton, yang terbaik yang dapat dilakukan tanpa menghentikan gerakannya ke depan adalah membuatnya melalui lubang melingkar dalam penghalang. Jika seseorang mengetahui waktu di mana foton dipancarkan (oleh laser, misalnya) dan waktu foton tiba di layar deteksi seperti kamera digital, maka dimungkinkan untuk menghitung waktu yang diperlukan untuk menempuh jarak itu dan waktu di mana foton melewati lubang. Namun demikian, untuk memungkinkan foton melewatinya, lubang melingkar harus memiliki diameter yang lebih besar daripada ukuran foton. Semakin kecil lubang melingkar yang dibuat, semakin dekat kita untuk mengetahui posisi foton yang tepat saat melewatinya. Namun, kita tidak akan pernah tahu apakah foton berada di luar pusat pada saat itu. Jika ukuran lubang persis sama dengan ukuran foton, maka foton tidak akan melewatinya. Ketika diameter lubang diperkecil, momentum atau arah foton saat meninggalkan lubang semakin berubah.

Niels Bohr dan rekan-rekannya berpendapat bahwa kita masuk ke dalam masalah besar jika kita menganggap benar hal-hal yang terlalu kecil untuk dilihat bahkan dengan mikroskop apa pun yang kita miliki buktinya hanya pada skala kehidupan sehari-hari. Dalam kehidupan sehari-hari, segala sesuatu memiliki posisi yang pasti setiap saat. Pada skala atom, kita tidak memiliki bukti untuk mendukung kesimpulan itu. Dalam kehidupan sehari-hari, segala sesuatu memiliki waktu yang pasti di mana mereka terjadi. Pada skala atom, kita tidak memiliki bukti untuk mendukung kesimpulan itu. Dalam kehidupan sehari-hari, jika seseorang mengamati sebuah pabrik dari shift malam hari pertama ke shift siang hari kedua dan seseorang melihat sebuah mobil yang sudah jadi digulirkan ke dermaga pengiriman, tidak masuk akal untuk mengatakan bahwa tidak mungkin untuk mengatakan apakah mobil itu dikirim selama shift malam atau selama shift siang. Tetapi pada skala atomik, kita dapat menunjukkan contoh-contoh ketika kita harus menghitung satu foton tunggal sebagai telah diproduksi pada dua waktu. (Jika itu tidak cukup buruk, kita juga dapat menunjukkan contoh di mana foton tunggal dihasilkan dari dua laser yang berdekatan).

Bagian dari kesulitan dalam mencari tahu apa yang terjadi pada skala atom adalah bahwa kita ingin mengetahui di mana sesuatu berada dan apa lintasannya, dan untuk mengetahui kedua hal tersebut untuk waktu yang sama, tetapi kita tidak dapat mengukur posisi dan lintasan pada saat yang sama. Kita mengukur momentum foton atau elektron pada satu waktu dan kemudian tanpa penundaan lebih dari yang diperlukan mengukur posisinya, atau kita mengalihkan hal-hal di sekitar dan mengukur posisi pertama dan momentum kedua. Masalahnya adalah bahwa dalam membuat yang pertama mengambil bentuk yang cukup pasti (dengan menekannya dengan cara tertentu) kita meningkatkan ketidakpastian yang terlibat dalam pengukuran berikutnya. Jika pengukuran awal kita begitu kasar sehingga banyak kesalahan yang diperkenalkan di masing-masing pengukuran, maka kita dapat memperbaiki hal-hal dengan menggunakan sentuhan yang lebih ringan untuk melakukan masing-masing pengukuran, tetapi kita tidak akan pernah bisa melampaui batas akurasi tertentu.

Kita tahu dari kehidupan sehari-hari bahwa mencoba menimbang sesuatu pada timbangan kamar mandi yang ditempatkan pada mesin cuci dalam siklus putaran akan menghasilkan hasil yang tidak akurat karena jarum pada timbangan akan bergoyang-goyang dengan buruk. Kita bisa mematikan mesin cuci. Tetapi untuk pengukuran yang sangat akurat, kami menemukan bahwa truk yang lewat di lingkungan sekitar membuat jarum timbangan bergoyang-goyang, jadi kami dapat meletakkan timbangan pada sesuatu untuk mengisolasinya dari gangguan luar. Kami percaya bahwa kami dapat menghilangkan getaran yang cukup untuk memberikan hasil seakurat yang kami inginkan. Kita tidak pernah menganggap bahwa benda pada timbangan itu sendiri bergetar atau memiliki momentum yang tidak terbatas.

Berargumen mundur dari Prinsip Ketidakpastian, tampaknya seolah-olah sebenarnya tidak ada posisi yang pasti dan tidak ada momentum yang pasti untuk hal skala atom apa pun, dan bahwa para peneliti hanya dapat memaksa hal-hal menjadi pasti dalam batas yang dinyatakan oleh Prinsip Ketidakpastian. Bohr dan rekan-rekannya hanya berargumen bahwa kita tidak dapat mengetahui apa pun tanpa melakukan pengukuran, dan ketika pengukuran dilakukan, kita dapat mendorong hal-hal ke arah posisi yang lebih pasti atau momentum yang lebih pasti, tetapi kita tidak bisa mendapatkan kepastian atau kepastian mutlak yang kita inginkan. Tetapi yang lain menganggap serius kemungkinan itu, dan berpendapat bahwa jika matematika benar maka tidak mungkin ada kepastian atau kepastian di dunia ultra kecil. Sifat sains adalah bahwa matematika hanyalah model realitas, dan tidak ada jaminan bahwa itu adalah model yang benar.

Matematika dan konsekuensi praktis dari hal-hal yang diprediksi oleh matematika sangat dapat diandalkan sehingga sangat sulit untuk tidak disetujui, tetapi apa yang dikatakan matematika tentang dunia nyata telah menghasilkan beberapa ide yang berbeda. Di antara para ilmuwan yang bekerja dengan Niels Bohr di Kopenhagen, prinsip ketidakpastian diambil untuk mengartikan bahwa pada tingkat dasar, alam semesta fisik tidak ada dalam bentuk deterministik. Sebaliknya, itu adalah kumpulan probabilitas atau potensi.

Berlawanan dengan cerita yang dijalin di sekitar matematika oleh kelompok Kopenhagen, ada cerita lain seperti "interpretasi alam semesta berganda" yang mengatakan bahwa setiap kali ada beberapa hasil yang mungkin menurut teori kuantum, setiap hasil terjadi di alam semesta barunya sendiri. Einstein berpendapat bahwa tidak ada beberapa kemungkinan hasil, jadi hanya ada satu alam semesta dan itu ditentukan, atau, seperti yang dia katakan, "Tuhan tidak bermain dadu."

Jika h adalah jumlah energi terkecil yang mungkin, maka persamaan dasar yang menunjukkan energi yang terkandung dalam foton dari berbagai frekuensi tidak akan seimbang. Itu akan salah.

Keberatan terhadap prinsip ketidakpastian

Albert Einstein melihat bahwa mekanika kuantum yang baru menyiratkan kurangnya posisi dan momentum dalam waktu sebelum pengukuran dilakukan, dan dia sangat keberatan. Dia sangat percaya bahwa segala sesuatu memiliki posisi yang pasti dan momentum yang pasti sebelum mereka diukur, dan bahwa fakta bahwa mengukur salah satu dari sepasang hal dan mengganggu kemungkinan mengukur yang lain secara akurat tidak membantah adanya kekurangan salah satu dari mereka sebelumnya. Dia dan dua rekannya menulis apa yang kemudian dikenal sebagai "makalah EPR". Makalah itu berpendapat bahwa pasti ada karakteristik yang menentukan posisi dan momentum, dan jika kita bisa melihatnya, atau jika kita bisa mendapatkan informasi tentang mereka, maka kita dapat secara matematis mengetahui dan memprediksi posisi dan momentum. Untuk waktu yang lama orang berpikir bahwa tidak ada cara untuk membuktikan atau menyangkal apa yang bagi Einstein merupakan artikel keyakinan. Argumen itu sangat produktif karena mengarah pada semua perkembangan modern dalam keterikatan.

Secara matematis, Einstein telah terbukti salah. Pada tahun 1964 John Stewart Bell mengembangkan metode matematika untuk membedakan antara perilaku dua partikel yang memiliki keadaan yang ditentukan yang hanya tidak diketahui oleh dua individu yang menyelidikinya, dan dua partikel yang memiliki keadaan terjerat yang tidak pasti atau tidak pasti sampai mereka diukur. Metodenya menunjukkan bahwa probabilitas untuk mendapatkan hasil tertentu berbeda di bawah dua asumsi yang berbeda. Karyanya disebut teorema Bell atau Ketidaksetaraan Bell. Eksperimen telah menunjukkan bahwa alam berperilaku seperti yang dijelaskan Bell.

Rute lain menuju ketidakpastian

Diskusi awal prinsip ketidakpastian Heisenberg bergantung pada model yang tidak mempertimbangkan bahwa partikel materi seperti elektron, proton, dll. memiliki panjang gelombang. Pada tahun 1926 Louis de Broglie menunjukkan bahwa semua hal, bukan hanya foton, memiliki frekuensinya sendiri. Benda-benda memiliki sifat gelombang dan sifat partikel, seperti halnya foton. Jika kita mencoba membuat gelombang benda seperti proton lebih sempit dan lebih tinggi, itu akan membuat posisinya lebih jelas, tetapi momentumnya akan menjadi kurang terdefinisi dengan baik. Jika kita mencoba membuat bagian momentum dari deskripsi gelombang lebih jelas, yaitu, membuatnya tetap dalam kisaran nilai yang lebih sempit, maka puncak gelombang menyebar dan posisinya menjadi kurang pasti.

Gelombang yang merupakan bagian dari deskripsi foton, dalam mekanika kuantum, bukanlah hal yang sama seperti gelombang di permukaan lautan atau daerah udara yang dimampatkan dan udara yang dijernihkan yang membentuk gelombang suara. Sebaliknya, gelombang ini memiliki puncak atau daerah amplitudo tinggi yang berkaitan dengan probabilitas menemukan sesuatu pada titik itu dalam ruang dan waktu. Lebih tepatnya, kuadrat amplitudo yang memberikan probabilitas munculnya beberapa fenomena.

Gelombang yang berlaku untuk foton mungkin merupakan gelombang sinus murni. Dalam hal ini, kuadrat nilai setiap puncak akan memberikan probabilitas untuk mengamati foton pada titik itu. Karena amplitudo gelombang sinus di mana-mana sama, probabilitas untuk menemukan foton pada masing-masing gelombang akan sama. Jadi, secara praktis, mengetahui gelombang untuk salah satu foton ini tidak akan memberikan petunjuk tentang di mana mencarinya. Di sisi lain, momentum foton secara matematis terkait dengan amplitudo gelombangnya. Karena dalam kasus ini kita memiliki gelombang sinus murni, amplitudo setiap siklus gelombang adalah sama dan oleh karena itu hanya ada satu nilai momentum yang terkait dengan gelombang ini. Kita tidak akan tahu di mana foton akan mengenai, tetapi kita akan tahu persis seberapa keras foton itu akan mengenai.

Dalam berkas cahaya yang fokus pada beberapa titik pada layar deteksi, gelombang yang terkait dengan foton bukanlah gelombang sinus murni. Sebaliknya, mereka adalah gelombang dengan amplitudo tinggi pada satu titik dan amplitudo yang jauh lebih rendah di kedua sisi puncak tertinggi itu. Secara matematis dimungkinkan untuk menganalisis gelombang seperti itu ke dalam sejumlah gelombang sinus yang berbeda dengan panjang gelombang yang berbeda. Sedikit lebih mudah untuk memvisualisasikan kebalikan dari proses ini dengan melihat gelombang sinus awal dari satu frekuensi yang ditambahkan gelombang sinus kedua dari panjang gelombang yang berbeda, kemudian gelombang ketiga, kemudian gelombang keempat, dan seterusnya. Hasilnya akan menjadi gelombang kompleks yang menunjukkan satu puncak tinggi dan mengandung sejumlah besar gelombang dengan panjang gelombang yang berbeda dan oleh karena itu memiliki momentum yang berbeda. Dalam hal ini, probabilitas bahwa foton akan muncul pada titik tertentu sangat tinggi, tetapi momentum yang diberikannya dapat berubah menjadi terkait dengan panjang gelombang dari salah satu gelombang komponen. Dengan kata lain, nilai p = ħ/λ bukan lagi nilai tunggal karena semua panjang "gelombang dengan panjang gelombang yang berbeda" harus diperhitungkan.

Simulasi ini menunjukkan bagaimana memodelkan secara matematis penajaman lokasi partikel: Menumpangkan banyak bentuk gelombang yang berbeda di atas gelombang sinus asli. Pusatnya akan membentuk puncak yang semakin tinggi, dan puncak-puncak lainnya akan meningkat jumlahnya tetapi menurun ketinggiannya karena mereka akan saling mengganggu satu sama lain. Jadi pada akhirnya ada banyak gelombang yang berbeda dalam superposisi, masing-masing dengan panjang gelombang yang berbeda dan (dengan p = ħ / λ) momentum yang berbeda, tetapi hanya satu puncak yang sangat tinggi, yang tumbuh lebih tinggi dan lebih sempit dan memberi kita sesuatu yang lebih dekat dan lebih dekat ke posisi yang menentukan.

Untuk membuat momentum semakin pasti, kita harus menghilangkan semakin banyak gelombang sinus yang ditumpangkan sampai kita hanya memiliki gelombang sinus sederhana yang tersisa. Dengan demikian, kita akan semakin mengurangi ketinggian puncak pusat dan secara progresif meningkatkan ketinggian tempat-tempat yang bersaing di mana seseorang mungkin menemukan partikel.

Jadi, ketika kita mulai dengan gambaran gelombang partikel subatomik, kita biasanya akan selalu berurusan dengan kasus-kasus dengan puncak pusat yang relatif tinggi dan panjang gelombang komponen yang relatif banyak. Tidak akan pernah ada posisi yang tepat atau momentum yang tepat yang diprediksi dalam keadaan ini. Jika model matematika adalah representasi akurat dari dunia nyata, maka tidak ada foton atau partikel subatomik lainnya yang memiliki posisi yang tepat atau momentum yang pasti. Ketika kita mengukur partikel seperti itu, kita dapat memilih metode yang lebih menekan puncak dan membuatnya lebih sempit, atau kita dapat memilih metode yang menurunkan puncak dan meratakan panjang gelombang komponen. Tergantung pada apa yang kita ukur dan bagaimana kita mengukurnya, kita dapat membuat lokasi kita keluar lebih pasti atau kita dapat membuat rentang momentum kita lebih sempit. Kita dapat berhati-hati dalam merancang eksperimen untuk menghindari berbagai cara menggoyangkan peralatan, tetapi kita tidak dapat menyingkirkan fakta bahwa tidak ada yang benar-benar pasti untuk memulai.

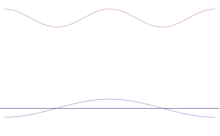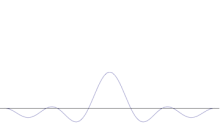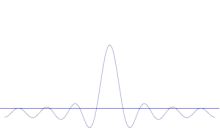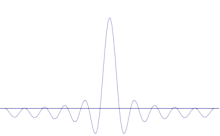
Superposisi dari beberapa gelombang bidang. Paket gelombang menjadi semakin terlokalisasi dengan penambahan banyak gelombang. Transformasi Fourier adalah operasi matematis yang memisahkan paket gelombang ke dalam gelombang bidang individualnya. Perhatikan bahwa gelombang yang ditunjukkan di sini adalah riil untuk tujuan ilustrasi saja, sedangkan dalam mekanika kuantum fungsi gelombang umumnya kompleks.

Pengaruh budaya

Pengaruh paling penting dari Prinsip Ketidakpastian Heisenberg adalah pada argumen tentang kebebasan kehendak. Di bawah teori-teori fisika klasik, adalah mungkin untuk berpendapat bahwa hukum sebab dan akibat tidak dapat dielakkan dan bahwa begitu alam semesta dimulai dengan cara tertentu, interaksi semua materi dan energi yang akan terjadi di masa depan dapat dihitung dari keadaan awal itu. Karena segala sesuatu secara mutlak merupakan hasil dari apa yang terjadi sebelumnya, mereka berpendapat, setiap keputusan yang dibuat manusia dan setiap situasi yang dimasuki manusia itu telah ditentukan sejak awal waktu. Maka kita tidak punya pilihan dalam apa yang kita lakukan.

Orang-orang yang percaya pada kebebasan kehendak berpendapat bahwa hukum mekanika kuantum tidak memprediksi apa yang akan terjadi, tetapi hanya apa yang lebih banyak dan apa yang lebih sedikit kemungkinannya untuk terjadi. Oleh karena itu, setiap tindakan adalah hasil dari serangkaian "lemparan koin" secara acak dan tidak ada keputusan yang dapat ditelusuri kembali ke seperangkat prasyarat yang diperlukan.

Ungkapan "lompatan kuantum" dan "lompatan kuantum" telah menjadi cara yang biasa untuk membicarakan sesuatu. Biasanya orang bermaksud menggambarkan sesuatu yang melibatkan perubahan besar yang terjadi dalam waktu singkat. Istilah ini sebenarnya berlaku untuk cara elektron berperilaku dalam atom baik ketika ia menyerap foton yang datang dari luar dan melompat dari satu orbit di sekitar inti atom ke orbit yang lebih tinggi, atau ketika ia memancarkan foton dan jatuh dari orbit yang lebih tinggi ke orbit yang lebih rendah. Gagasan Neils Bohr dan rekan-rekannya adalah bahwa elektron tidak bergerak di antara orbit, melainkan menghilang dari satu orbit dan seketika muncul di orbit lain. Jadi, lompatan kuantum sebenarnya bukanlah perubahan yang menghancurkan bumi, tetapi perubahan kecil yang tiba-tiba dari satu domain ke domain lainnya.

Ketika manusia mengukur beberapa proses pada skala subatomik dan prinsip ketidakpastian terwujud, maka tindakan manusia dapat dikatakan telah mempengaruhi hal yang sedang diukur. Melakukan pengukuran yang dimaksudkan untuk mendapatkan indikasi pasti tentang lokasi partikel pasti akan mempengaruhi momentumnya dan apa pun yang dilakukan untuk mengukur momentum itu sesegera mungkin setelah mengukur posisinya, probabilitas momentum apa yang akan ditemukan tidak dapat gagal untuk telah diubah. Jadi prinsip ketidakpastian dapat menjelaskan beberapa jenis gangguan yang dihasilkan oleh penyelidik yang mempengaruhi hasil eksperimen atau pengamatan. Namun, tidak semua efek pengamat disebabkan oleh efek kuantum atau prinsip ketidakpastian. Sisanya adalah "efek pengamat" tetapi bukan efek ketidakpastian kuantum.

Efek-efek pengamat meliputi segala macam hal yang beroperasi pada skala kejadian manusia biasa. Jika seorang antropolog mencoba untuk mendapatkan gambaran yang jelas tentang kehidupan dalam masyarakat primitif tetapi kehadirannya mengganggu masyarakat yang dikunjunginya, maka pengamatan yang dilakukan mungkin sangat menyesatkan. Namun, tidak ada interaksi yang relevan terjadi pada tingkat yang dijelaskan oleh mekanika kuantum atau prinsip ketidakpastian.

Kadang-kadang kata "quantum" akan digunakan untuk tujuan periklanan untuk mengindikasikan sesuatu yang baru dan kuat. Contohnya, produsen motor bensin kecil, Briggs and Stratton, memiliki satu lini motor empat silinder berkekuatan kuda rendah untuk mesin pemotong rumput berbahan bakar bensin dan perkakas taman serupa yang disebut "Quantum."

Baca lebih lanjut

• Memperkenalkan Teori Kuantum, hal. 115 dan hal. 158

J.P. McEvoy dan Oscar Zarate