Konstanta Planck

Latar Belakang

Simbol yang digunakan dalam artikel ini.
Simbol Arti E Energi h Konstanta Planck k Konstanta Boltzmann c kecepatan cahaya λ panjang gelombang radiasi ν frekuensi radiasi T suhu absolut

Antara tahun 1670 dan 1900, para ilmuwan mendiskusikan sifat cahaya. Sebagian ilmuwan meyakini bahwa cahaya terdiri atas jutaan partikel kecil. Ilmuwan lain percaya bahwa cahaya adalah gelombang.

Cahaya: gelombang atau partikel?

Pada tahun 1678, Christiaan Huygens menulis buku Traité de la lumiere ("Risalah tentang cahaya"). Dia percaya bahwa cahaya terdiri dari gelombang. Dia mengatakan bahwa cahaya tidak dapat terdiri dari partikel karena cahaya dari dua balok tidak saling memantul. Pada tahun 1672, Isaac Newton menulis buku Opticks. Dia percaya bahwa cahaya terdiri dari partikel merah, kuning, dan biru yang disebutnya corpusles. Newton menjelaskan hal ini dengan "eksperimen dua prisma". Prisma pertama memecah cahaya menjadi warna-warna yang berbeda. Prisma kedua menggabungkan warna-warna ini kembali menjadi cahaya putih.

Selama abad ke-18, teori Newton paling banyak mendapat perhatian. Pada tahun 1803, Thomas Young menggambarkan "eksperimen celah ganda". Dalam eksperimen ini, cahaya yang melalui dua celah sempit berinterferensi dengan dirinya sendiri. Hal ini menyebabkan pola yang menunjukkan bahwa cahaya terdiri dari gelombang. Selama sisa abad kesembilan belas, teori gelombang cahaya paling banyak mendapat perhatian. Pada tahun 1860-an, James Clerk Maxwell mengembangkan persamaan yang menggambarkan radiasi elektromagnetik sebagai gelombang.

Teori radiasi elektromagnetik memperlakukan cahaya, gelombang radio, gelombang mikro, dan banyak jenis gelombang lainnya sebagai hal yang sama, kecuali bahwa mereka memiliki panjang gelombang yang berbeda. Panjang gelombang cahaya yang dapat kita lihat dengan mata kita kira-kira antara 400 dan 600 nm. Panjang gelombang gelombang radio bervariasi dari 10 m hingga 1500 m dan panjang gelombang gelombang mikro sekitar 2 cm. Dalam ruang hampa udara, semua gelombang elektromagnetik bergerak dengan kecepatan cahaya. Frekuensi gelombang elektromagnetik diberikan oleh:

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}} .

Simbol-simbol didefinisikan di sini.

Radiator tubuh hitam

Semua benda hangat mengeluarkan radiasi termal, yang merupakan radiasi elektromagnetik. Untuk sebagian besar benda di Bumi, radiasi ini berada dalam kisaran infra-merah, tetapi sesuatu yang sangat panas (1000 °C atau lebih), mengeluarkan radiasi yang terlihat, yaitu cahaya. Pada akhir tahun 1800-an, banyak ilmuwan mempelajari panjang gelombang radiasi elektromagnetik dari radiator benda hitam pada suhu yang berbeda.

Hukum Rayleigh-Jeans

Lord Rayleigh pertama kali menerbitkan dasar-dasar hukum Rayleigh-Jeans pada tahun 1900. Teori ini didasarkan pada teori kinetik gas. Sir James Jeans menerbitkan teori yang lebih lengkap pada tahun 1905. Hukum ini menghubungkan kuantitas dan panjang gelombang energi elektromagnetik yang dilepaskan oleh radiator benda hitam pada suhu yang berbeda. Persamaan yang menjelaskan hal ini adalah:

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}} .

Untuk radiasi panjang gelombang panjang, hasil yang diprediksi oleh persamaan ini sesuai dengan hasil praktis yang diperoleh di laboratorium. Namun, untuk panjang gelombang pendek (sinar ultraviolet) perbedaan antara teori dan praktik begitu besar sehingga mendapat julukan "bencana ultra-violet".

Hukum Planck

pada tahun 1895 Wien mempublikasikan hasil studinya tentang radiasi dari benda hitam. Rumusnya adalah:

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda kT}}}} .

Formula ini bekerja dengan baik untuk radiasi elektromagnetik panjang gelombang pendek, tetapi tidak bekerja dengan baik dengan panjang gelombang panjang.

Pada tahun 1900 Max Planck mempublikasikan hasil studinya. Dia mencoba mengembangkan ekspresi untuk radiasi benda-hitam yang dinyatakan dalam istilah panjang gelombang dengan mengasumsikan bahwa radiasi terdiri dari kuanta kecil dan kemudian melihat apa yang terjadi jika kuanta dibuat kecil tak terhingga (Ini adalah pendekatan matematis standar). Ekspresinya adalah:

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}~{\frac {1}{e^{\frac {hc}{\lambda kT}}-1}}}} .

Jika panjang gelombang cahaya dibiarkan menjadi sangat besar, maka dapat ditunjukkan bahwa hubungan Raleigh-Jeans dan Planck hampir identik.

Ia menghitung h dan k dan menemukan bahwa

h = 6,55×10⁻²⁷ erg-sec.

k = 1.34×10⁻¹⁶ erg-deg^-1 .

Nilai-nilai ini dekat dengan nilai yang diterima saat ini, masing-masing 6,62606×10⁻³⁴ dan 1,38065×10⁻¹⁶ . Hukum Planck sangat sesuai dengan data eksperimen, tetapi signifikansi penuhnya baru dihargai beberapa tahun kemudian.

Teori kuantum cahaya

Ternyata, elektron akan terlepas oleh efek fotolistrik jika cahaya mencapai frekuensi ambang. Di bawah ini tidak ada elektron yang dapat dipancarkan dari logam. Pada tahun 1905 Albert Einstein menerbitkan sebuah makalah yang menjelaskan efek tersebut. Einstein mengusulkan bahwa seberkas cahaya bukanlah gelombang yang merambat melalui ruang, melainkan kumpulan paket gelombang diskrit (foton), masing-masing dengan energi. Einstein mengatakan bahwa efeknya disebabkan oleh foton yang menabrak elektron. Ini menunjukkan sifat partikel cahaya.

Einstein juga menemukan bahwa radiasi elektromagnetik dengan panjang gelombang yang panjang tidak berpengaruh. Einstein mengatakan bahwa hal ini disebabkan karena "partikel" tersebut tidak memiliki energi yang cukup untuk mengganggu elektron.

Plank menyarankan bahwa energi setiap foton terkait dengan frekuensi foton oleh konstanta Planck. Ini dapat ditulis secara matematis sebagai:

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }}} .

Plank menerima Hadiah Nobel pada tahun 1918 sebagai pengakuan atas jasa-jasa yang diberikannya untuk kemajuan Fisika dengan penemuannya tentang kuanta energi. Pada tahun 1921 Einstein menerima Hadiah Nobel karena menghubungkan konstanta Planck dengan efek fotolistrik.

Ilustrasi diambil dari surat asli Newton kepada Royal Society (1 Januari 1671 [kalender Julian]). S mewakili cahaya matahari. Cahaya antara bidang BC dan DE berwarna. Warna-warna ini digabungkan kembali untuk membentuk cahaya matahari pada bidang GH


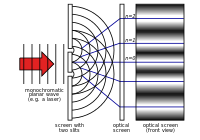
Eksperimen celah ganda Young


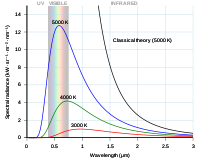
Kurva Rayleigh-Jeans dan kurva Planck diplot terhadap panjang gelombang foton.


Konferensi Solway 1911. Planck, Einstein dan Jeans berdiri. Planck kedua dari kiri. Einstein kedua dari kanan. Jeans kelima dari kanan. Wien duduk, ketiga dari kanan

Aplikasi

Konstanta Planck penting dalam banyak aplikasi. Beberapa di antaranya tercantum di bawah ini.

Model atom Bohr

Pada tahun 1913 Niels Bohr menerbitkan model Bohr dari struktur atom. Bohr mengatakan bahwa momentum sudut elektron yang mengelilingi inti hanya dapat memiliki nilai tertentu. Nilai-nilai ini diberikan oleh persamaan

L = n h 2 π {\displaystyle L=n{\frac {h}{2\pi }}}}

di mana

L = momentum sudut yang terkait dengan suatu level.

n = bilangan bulat positif.

h = Konstanta Planck.

Model Bohr dari atom dapat digunakan untuk menghitung energi elektron pada setiap tingkat. Elektron biasanya akan mengisi keadaan bernomor terendah dari sebuah atom. Jika atom menerima energi dari, misalnya, arus listrik, elektron akan tereksitasi ke keadaan yang lebih tinggi. Elektron kemudian akan turun kembali ke keadaan yang lebih rendah dan akan kehilangan energi ekstra mereka dengan mengeluarkan foton. Karena tingkat energi memiliki nilai tertentu, foton akan memiliki tingkat energi tertentu. Cahaya yang dipancarkan dengan cara ini dapat dipecah menjadi warna-warna yang berbeda dengan menggunakan prisma. Setiap elemen memiliki polanya sendiri. Pola untuk neon ditunjukkan di samping.

Prinsip ketidakpastian Heisenberg

Pada tahun 1927 Werner Heisenberg menerbitkan prinsip ketidakpastian. Prinsip ini menyatakan bahwa tidak mungkin melakukan pengukuran tanpa mengganggu hal yang sedang diukur. Prinsip ini juga memberi batas pada gangguan minimum yang disebabkan oleh melakukan pengukuran.

Dalam dunia makroskopik, gangguan-gangguan ini membuat perbedaan yang sangat kecil. Misalnya, jika suhu labu cairan diukur, termometer akan menyerap sejumlah kecil energi saat memanas. Hal ini akan menyebabkan kesalahan kecil dalam pembacaan akhir, tetapi kesalahan ini kecil dan tidak penting.

Dalam mekanika kuantum, ada hal yang berbeda. Beberapa pengukuran dilakukan dengan melihat pola foton yang tersebar. Salah satu contohnya adalah hamburan Compton. Jika posisi dan momentum partikel sedang diukur, prinsip ketidakpastian menyatakan bahwa ada trade-off antara keakuratan pengukuran momentum dan keakuratan pengukuran posisi. Persamaan yang menggambarkan trade-off ini adalah:

Δ x Δ p ≳ h {\displaystyle \Delta x\,\Delta p\gtrsim h\qquad \qquad \qquad }

di mana

Δp = ketidakpastian dalam momentum.

Δx = ketidakpastian dalam posisi.

h = Konstanta Planck.

Warna dioda pemancar cahaya

Dalam sirkuit listrik yang ditunjukkan di sebelah kanan, penurunan tegangan di seluruh dioda pemancar cahaya (LED) tergantung pada bahan LED. Untuk dioda silikon, penurunannya adalah 0,6 V. Namun, untuk LED, penurunannya antara 1,8 V dan 2,7 V. Informasi ini memungkinkan pengguna untuk menghitung konstanta Planck.

Energi yang dibutuhkan satu elektron untuk melompati penghalang potensial dalam bahan LED diberikan oleh

E = Q e V L {\displaystyle E=Q_{e}V_{L}}, }

di mana

Q_e adalah muatan pada satu elektron.

V_L adalah penurunan tegangan pada LED.

Ketika elektron meluruh kembali, ia memancarkan satu foton cahaya. Energi foton diberikan oleh persamaan yang sama yang digunakan dalam efek fotolistrik. Jika persamaan-persamaan ini digabungkan, panjang gelombang cahaya dan tegangan dihubungkan oleh

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}}}\}

Tabel di bawah ini bisa dihitung dari hubungan ini.

Warna	Panjang gelombang (nm)	Tegangan
lampu merah	650	1.89
lampu hijau	550	2.25
cahaya biru	470	2.62

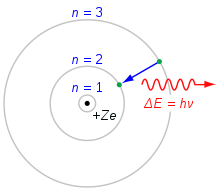
Model atom Bohr. Elektron yang jatuh dari kulit n = 3 ke kulit n = 2 kehilangan energi. Energi ini terbawa sebagai foton tunggal.


Spektrum Neon yang terlihat. Tiap garis mewakili pasangan tingkat energi yang berbeda.


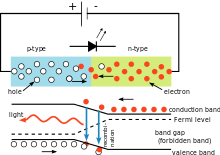
Rangkaian LED sederhana yang menggambarkan penggunaan konstanta Planck. Warna cahaya yang dipancarkan tergantung pada penurunan tegangan di seluruh dioda. Panjang gelombang cahaya dapat dihitung menggunakan konstanta Planck.

Nilai konstanta Planck dan redefinisi kilogram

Sejak penemuannya, pengukuran h menjadi jauh lebih baik. Planck pertama kali mengutip nilai h menjadi 6,55×10⁻²⁷ erg-sec. Nilai ini berada dalam 5% dari nilai saat ini.

Pada tanggal 3 Maret 2014, pengukuran terbaik h dalam satuan SI adalah 6,62606957×10⁻³⁴ J-s. Angka ekuivalen dalam satuan cgs adalah 6,62606957×10⁻²⁷ erg-sec. Ketidakpastian relatif h adalah 4,4×10⁻⁸ .

Konstanta Planck tereduksi (ħ) adalah nilai yang kadang-kadang digunakan dalam mekanika kuantum. Ini didefinisikan oleh

ℏ = h 2 π {\displaystyle \hbar ={\frac {h}{2\pi }}} .

Satuan Planck terkadang digunakan dalam mekanika kuantum, bukan SI. Dalam sistem ini konstanta Planck tereduksi memiliki nilai 1, sehingga nilai konstanta Planck adalah 2π.

Konstanta Plancks sekarang dapat diukur dengan presisi yang sangat tinggi. Hal ini menyebabkan BIPM mempertimbangkan definisi baru untuk kilogram. Prototipe kilogram internasional tidak lagi digunakan untuk mendefinisikan kilogram. Sebaliknya, BIPM mendefinisikan konstanta Planck memiliki nilai yang tepat. Para ilmuwan menggunakan nilai ini dan definisi meter dan detik untuk mendefinisikan kilogram.

 

Nilai Konstanta Planck Teoretis

Konstanta Planck juga dapat diturunkan secara matematis:

 

h = μ 0 π 12 c 3 [ q 0 [ 0.9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6.63 × 10 - 34 J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{{3}}}{[{q_{0}}}{[0.9163a_{0}]}^{2}]^{2}}{f_{1r}}^{5}\cdot {s}=6.63\times 10^{-34}J\cdot s}

Di sini, μ 0 {\displaystyle \mu _{0}} adalah permeabilitas ruang bebas, c {\displaystyle c} adalah kecepatan cahaya, q 0 {\displaystyle q_{0}} adalah muatan listrik elektron, a 0 {\displaystyle a_{0}} adalah jari-jari Bohr, dan f 1 r {\displaystyle f_{1r}} adalah frekuensi revolusi elektron dalam atom hidrogen (f 1 r = 3.29 × 10 15 r e v / s ) {\displaystyle (f_{1r}=3.29\times 10^{{15}rev/s)} . Ketika nilai-nilai konstanta ini disubstitusikan ke konstanta Planck teoritis, nilai konstanta Planck teoritis persis sama dengan nilai eksperimen.

Halaman terkait

• Dualitas gelombang-partikel