Probabilitas
Probabilitas adalah bagian dari matematika terapan. Probabilitas berkaitan dengan peluang, studi tentang hal-hal yang mungkin terjadi atau mungkin tidak terjadi.
Misalnya, dengan menggunakan probabilitas, Anda dapat menunjukkan bahwa jika Anda melempar koin ke udara dan membiarkannya mendarat, separuh waktu koin akan mendarat dengan satu sisi menghadap ke atas, dan separuh waktu lagi dengan sisi lain menghadap ke atas. Banyak koin memiliki gambar wajah orang terkenal di satu sisi, dan sesuatu yang lain di sisi lainnya. Seringkali orang menyebut sisi yang bergambar wajah sebagai "kepala", dan sisi lainnya sebagai "ekor".
Probabilitas (p) dari suatu peristiwa selalu antara nol (tidak mungkin) dan satu (pasti).
Jika kita melempar sebuah dadu (jamak: dadu), maka peluang bahwa dadu itu akan mendarat pada angka 1 adalah 1/6 (Ini karena ada 6 angka pada sebuah dadu). Juga, peluangnya akan mendarat pada angka 2 adalah 1/6. Ini karena ia bisa mendarat pada 1, 2, 3, 4, 5, atau 6. Peluang angka antara 1 dan 6 mendarat adalah 1. Setiap kali kita melempar dadu, dadu akan selalu mendarat pada angka antara 1 dan 6.
Probabilitas dapat diketahui dengan menggunakan matematika. Misalnya, jika Anda melempar enam dadu, peluang Anda mendapatkan angka lebih dari sepuluh tidak jelas, tetapi dapat diketahui dengan menggunakan matematika dan sains.
Salah satu hal yang paling menarik tentang peluang adalah bahwa untuk mengetahui probabilitas bahwa dua hal akan terjadi, Anda mengalikan kedua probabilitasnya bersama-sama. Sebagai contoh, misalkan Anda ingin mengetahui probabilitas melempar dua dadu dan mendapatkan kombinasi tertentu (bisa dua angka 6 atau angka 3 lalu angka 5, dua angka saja). Kemungkinan mendapatkan angka 3 adalah satu banding enam (⅙) dan kemungkinan mendapatkan angka 5 juga satu banding enam, jadi peluang mendapatkan angka 3 kemudian angka 5 adalah ⅙ × ⅙ = ⅟36. Jika angka itu dinyatakan sebagai angka antara 0 dan 1, maka sama dengan 0.027...7, yang cukup rendah. Kemungkinan mendapatkan angka 3, lalu 5, dan kemudian 2 adalah ⅙×⅙×⅙×⅙=⅟216 atau 0.00463, yang merupakan probabilitas yang jauh lebih rendah.
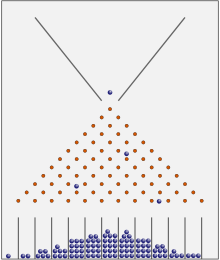
Dalam mesin kacang atau kotak Galton, sebagian besar bola berakhir dekat dengan pusat. Dalam jangka panjang, mereka akan menunjukkan distribusi normal
Ide-ide probabilitas
Orang-orang seperti Jacob Bernoulli, Pierre-Simon Laplace, atau Christiaan Huygens menggunakan kata probabilitas, seperti yang dijelaskan di atas. Orang lain berpikir tentang frekuensi; pengertian probabilitas biasanya disebut Probabilitas frekuensi.
Halaman terkait
- Daftar topik matematika
- Teori probabilitas
| Kontrol otoritas |
|
Pertanyaan dan Jawaban
T: Apa itu probabilitas?
J: Probabilitas adalah bagian dari matematika terapan yang mempelajari hal-hal yang mungkin terjadi atau tidak mungkin terjadi.
T: Bagaimana probabilitas dapat dinyatakan?
A: Probabilitas dapat dinyatakan sebagai angka antara nol (tidak mungkin) dan satu (pasti).
T: Apa contoh penggunaan probabilitas?
A: Contoh penggunaan probabilitas adalah menunjukkan bahwa dengan melempar koin ke udara dan membiarkannya mendarat, separuh dari waktu koin akan mendarat dengan satu sisi menghadap ke atas, dan separuhnya lagi dengan sisi lainnya menghadap ke atas.
T: Bagaimana cara menghitung probabilitas melempar dua dadu dan mendapatkan kombinasi tertentu?
J: Untuk menghitung probabilitas melempar dua dadu dan mendapatkan kombinasi tertentu, Anda harus mengalikan kedua probabilitasnya. Contohnya, jika Anda ingin mengetahui kemungkinan mendapatkan angka 3 dan angka 5, maka caranya adalah 1/6 x 1/6 = 1/36.
T: Apa yang dimaksud dengan "ekor" saat berbicara tentang koin?
J: Ketika berbicara tentang koin, "ekor" mengacu pada sisi tanpa wajah atau gambar di atasnya.
T: Seberapa besar kemungkinan melempar enam dadu dan mendapatkan angka lebih dari sepuluh? J: Kemungkinan melempar enam dadu dan mendapatkan angka lebih dari sepuluh dapat diketahui dengan menggunakan matematika dan sains, tetapi tidak jelas.
T: Apa yang terjadi jika Anda mengalikan dua probabilitas secara bersamaan?
J: Ketika Anda mengalikan dua probabilitas bersama-sama, Anda menghitung peluang kedua hal tersebut akan terjadi sekaligus.
Cari di dalam ensiklopedia