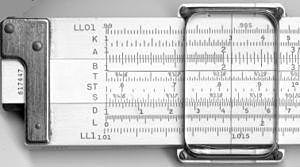
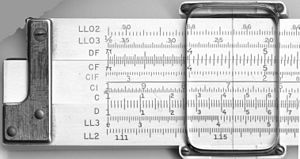
Aturan geser

Konsep dasar

Dalam bentuknya yang paling dasar, aturan geser menggunakan dua skala logaritmik untuk memungkinkan perkalian dan pembagian angka dengan cepat. Operasi-operasi umum ini bisa memakan waktu dan rawan kesalahan bila dilakukan di atas kertas. Aturan geser yang lebih kompleks memungkinkan perhitungan lain, seperti akar kuadrat, eksponensial, logaritma, dan fungsi trigonometri.

Perhitungan matematis dilakukan dengan menyejajarkan tanda pada strip tengah geser dengan tanda pada salah satu strip tetap. Posisi relatif dari tanda lainnya kemudian dapat diamati. Angka-angka yang disejajarkan dengan tanda memberikan nilai perkiraan dari hasil kali, hasil bagi, atau hasil perhitungan lainnya.

Pengguna menentukan lokasi titik desimal dalam hasil, berdasarkan estimasi mental. Notasi ilmiah digunakan untuk melacak titik desimal dalam perhitungan yang lebih formal. Langkah-langkah penjumlahan dan pengurangan dalam suatu perhitungan umumnya dilakukan secara mental atau di atas kertas, bukan pada slide rule.

Sebagian besar slide rules memiliki tiga strip linier dengan panjang yang sama. Strip-strip ini disejajarkan secara paralel dan saling mengunci, sehingga strip tengah bisa digerakkan secara memanjang relatif terhadap dua strip lainnya. Dua strip terluar ditetapkan sehingga posisi relatifnya tidak berubah.

Beberapa slide rules ("duplex" model) memiliki skala pada kedua sisi rule dan slide strip, yang lainnya pada satu sisi strip luar dan kedua sisi slide strip, yang lainnya lagi pada satu sisi saja ("simplex" rules). Kursor geser dengan garis penyelarasan vertikal digunakan untuk menemukan titik-titik yang bersesuaian pada skala yang tidak bersebelahan atau, dalam model dupleks, berada di sisi lain dari aturan. Kursor juga bisa merekam hasil antara pada salah satu skala.

Kursor pada aturan geser

Menggunakan aturan geser untuk penghitungan

Perkalian

Sebuah logaritma mentransformasikan operasi perkalian dan pembagian menjadi penjumlahan dan pengurangan menurut aturan log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=\log(x)+\log(y)} dan log ( x / y ) = log ( x ) - log ( y ) {\displaystyle \log(x/y)=\log(x)-\log(y)} . Memindahkan skala atas ke kanan dengan jarak log ( x ) {\displaystyle \log(x)} , dengan mencocokkan awal skala atas dengan label x {\displaystyle x} pada bagian bawah, menyelaraskan setiap angka y {\displaystyle y}  pada skala atas, dengan angka pada posisi log ( x ) + log ( y ) {\displaystyle \log(x)+\log(y)} pada skala bawah. Karena log ( x ) + log ( y ) = log ( x y ) {\displaystyle \log(x)+\log(y)=\log(xy)} , posisi ini pada skala bawah memberikan x y {\displaystyle xy} , hasil kali x {\displaystyle x} dan y {\displaystyle y} . Misalnya, untuk menghitung 3*2, 1 pada skala atas dipindahkan ke 2 pada skala bawah. Jawabannya, 6, dibaca dari skala bawah di mana 3 berada pada skala atas. Secara umum, 1 pada bagian atas dipindahkan ke faktor di bagian bawah, dan jawabannya dibaca dari bagian bawah di mana faktor lainnya berada di bagian atas.

Operasi mungkin "keluar dari skala;" misalnya, diagram di atas menunjukkan bahwa aturan geser belum memposisikan angka 7 pada skala atas di atas angka apa pun pada skala bawah, sehingga tidak memberikan jawaban apa pun untuk 2×7. Dalam kasus seperti itu, pengguna dapat menggeser skala atas ke kiri sampai indeks kanannya sejajar dengan 2, yang secara efektif mengalikan dengan 0,2, bukan dengan 2, seperti pada ilustrasi di bawah ini:

Di sini pengguna aturan geser harus ingat untuk menyesuaikan titik desimal dengan tepat untuk mengoreksi jawaban akhir. Kita ingin mencari 2×7, tetapi kita malah menghitung 0,2×7=1,4. Jadi jawaban yang benar bukanlah 1,4 tetapi 14. Menyetel ulang slide bukan satu-satunya cara untuk menangani perkalian yang akan menghasilkan hasil di luar skala, seperti 2×7; beberapa metode lainnya adalah:

• (1) Gunakan skala dua dekade A dan B.
• (2) Gunakan skala yang dilipat. Dalam contoh ini, tetapkan 1 kiri dari C yang berlawanan dengan 2 dari D. Pindahkan kursor ke 7 pada CF, dan baca hasilnya dari DF.
• (3) Gunakan skala CI terbalik. Posisikan angka 7 pada skala CI di atas angka 2 pada skala D, kemudian baca hasilnya dari skala D, di bawah angka 1 pada skala CI. Karena 1 muncul di dua tempat pada skala CI, salah satunya akan selalu berada pada skala.
• (4) Gunakan skala CI terbalik dan skala C. Sejajarkan 2 dari CI dengan 1 dari D, dan baca hasilnya dari D, di bawah angka 7 pada skala C.

Metode 1 mudah dimengerti, tetapi memerlukan hilangnya presisi. Metode 3 memiliki keuntungan karena hanya melibatkan dua skala.

Divisi

Ilustrasi di bawah ini mendemonstrasikan perhitungan 5.5/2. Angka 2 pada skala atas ditempatkan di atas 5.5 pada skala bawah. Angka 1 pada skala atas terletak di atas hasil bagi, 2,75. Ada lebih dari satu metode untuk melakukan pembagian, tetapi metode yang disajikan di sini memiliki keuntungan bahwa hasil akhir tidak boleh di luar skala, karena seseorang memiliki pilihan untuk menggunakan 1 di kedua ujungnya.

Operasi lainnya

Selain skala logaritmik, beberapa slide rules memiliki fungsi matematika lainnya yang dikodekan pada skala tambahan lainnya. Yang paling populer adalah trigonometri, biasanya sinus dan tangen, logaritma umum (log10) (untuk mengambil log nilai pada skala pengali), logaritma natural (ln) dan skala eksponensial (e^x ). Beberapa aturan termasuk skala Pythagoras, untuk menghitung sisi-sisi segitiga, dan skala untuk menghitung lingkaran. Yang lainnya menampilkan skala untuk menghitung fungsi hiperbolik. Pada aturan linear, skala dan pelabelannya sangat terstandardisasi, dengan variasi yang biasanya terjadi hanya dalam hal skala mana yang disertakan dan dalam urutan apa:

A, B	skala logaritmik dua dekade, digunakan untuk menemukan akar kuadrat dan kuadrat angka
C, D	skala logaritmik satu dekade
K	skala logaritmik tiga dekade, digunakan untuk menemukan akar pangkat tiga dan kubus bilangan
CF, DF	Versi "terlipat" dari skala C dan D yang dimulai dari π dan bukan dari kesatuan; ini akan memudahkan dalam dua kasus. Pertama, ketika pengguna menebak suatu produk akan mendekati 10 tetapi tidak yakin apakah akan sedikit kurang atau sedikit lebih dari 10, skala yang dilipat menghindari kemungkinan keluar dari skala. Kedua, dengan membuat awal π dan bukan akar kuadrat dari 10, mengalikan atau membagi dengan π (seperti yang umum dalam rumus sains dan teknik) disederhanakan.
CI, DI, DIF	Skala "terbalik", berjalan dari kanan ke kiri, digunakan untuk menyederhanakan langkah 1/x
S	digunakan untuk menemukan sinus dan kosinus pada skala D
T	digunakan untuk menemukan garis singgung dan kotangen pada skala D dan DI
ST, SRT	digunakan untuk sinus dan tangen sudut kecil dan konversi derajat-radian
L	skala linear, digunakan bersama dengan skala C dan D untuk menemukan logaritma basis-10 dan pangkat 10
LLn	seperangkat skala log-log, digunakan untuk menemukan logaritma dan eksponensial angka
Ln	skala linear, digunakan bersama dengan skala C dan D untuk menemukan logaritma natural (basis e) dan e x {\displaystyle e^{x}}

 

Timbangan di bagian depan dan belakang slide rule K&E 4081-3.

Aturan Geser Biner yang diproduksi oleh Gilson pada tahun 1931 melakukan fungsi penjumlahan dan pengurangan terbatas pada pecahan.

Akar dan kekuatan

Ada skala satu dekade (C dan D), dua dekade (A dan B), dan tiga dekade (K). Untuk menghitung x 2 {\displaystyle x^{2}} misalnya, cari x pada skala D dan baca kuadratnya pada skala A. Membalikkan proses ini memungkinkan akar kuadrat ditemukan, dan sama halnya untuk pangkat 3, 1/3, 2/3, dan 3/2. Perhatian harus diberikan ketika basis, x, ditemukan di lebih dari satu tempat pada skalanya. Misalnya, ada dua angka sembilan pada skala A; untuk menemukan akar kuadrat dari sembilan, gunakan yang pertama; yang kedua memberikan akar kuadrat dari 90.

Untuk masalah x y {\displaystyle x^{y}} , gunakan skala LL. Bila ada beberapa skala LL, gunakan skala dengan x di atasnya. Pertama, sejajarkan 1 paling kiri pada skala C dengan x pada skala LL. Kemudian, temukan y pada skala C dan turunkan ke skala LL dengan x di atasnya. Skala itu akan menunjukkan jawabannya. Jika y adalah "di luar skala," cari x y / 2 {\displaystyle x^{y/2}} dan kuadratkan dengan menggunakan skala A dan B seperti yang dijelaskan di atas.

Trigonometri

Skala S, T, dan ST digunakan untuk fungsi trigonometri dan kelipatan fungsi trig, untuk sudut dalam derajat. Banyak slide rules memiliki skala S, T, dan ST yang ditandai dengan derajat dan menit. Apa yang disebut model decitrig menggunakan pecahan desimal derajat sebagai gantinya.

Logaritma dan eksponensial

Logaritma dan eksponensial basis-10 ditemukan dengan menggunakan skala L, yang linier. Beberapa aturan geser memiliki skala Ln, yaitu untuk basis e.

Skala Ln ditemukan oleh seorang siswa kelas 11, Stephen B. Cohen, pada tahun 1958. Maksud aslinya adalah untuk memungkinkan pengguna memilih eksponen x (dalam rentang 0 hingga 2,3) pada skala Ln dan membaca e^x pada skala C (atau D) dan e^–x pada skala CI (atau DI). Pickett, Inc. diberi hak eksklusif untuk skala tersebut. Belakangan, penemu menciptakan seperangkat "tanda" pada skala Ln untuk memperluas jangkauan di luar batas 2,3, tetapi Pickett tidak pernah memasukkan tanda-tanda ini pada aturan gesernya. ^[]

Penjumlahan dan pengurangan

Aturan geser biasanya tidak digunakan untuk penjumlahan dan pengurangan, tetapi tetap memungkinkan untuk melakukannya dengan menggunakan dua teknik yang berbeda.

Metode pertama untuk melakukan penjumlahan dan pengurangan pada C dan D (atau skala yang sebanding) memerlukan pengubahan masalah menjadi salah satu pembagian. Untuk penjumlahan, hasil bagi dari dua variabel ditambah satu kali pembagi sama dengan jumlah mereka:

x + y = ( x y + 1 ) y {\displaystyle x+y=\left({\frac {x}{y}}+1\right)y}

Untuk pengurangan, hasil bagi dari dua variabel dikurangi satu kali pembagi sama dengan selisihnya:

x - y = ( x y - 1 ) y {\displaystyle x-y=\left({\frac {x}{y}}}-1\right)y}

Metode ini mirip dengan teknik penambahan/pengurangan yang digunakan untuk sirkuit elektronik berkecepatan tinggi dengan sistem bilangan logaritmik dalam aplikasi komputer khusus seperti superkomputer Gravity Pipe (GRAPE) dan model Markov tersembunyi.

Metode kedua menggunakan skala L linear geser yang tersedia pada beberapa model. Penjumlahan dan pengurangan dilakukan dengan menggeser kursor ke kiri (untuk pengurangan) atau ke kanan (untuk penambahan) kemudian mengembalikan slide ke 0 untuk membaca hasilnya.

Desain fisik

Aturan linear standar

Panjang aturan geser dikutip dalam hal panjang nominal timbangan. Timbangan pada model "10 inci" yang paling umum sebenarnya memiliki panjang 25 cm, karena dibuat dengan standar metrik, meskipun beberapa aturan menawarkan timbangan yang sedikit diperpanjang untuk menyederhanakan manipulasi ketika hasilnya meluap. Aturan saku biasanya 5 inci. Model yang panjangnya beberapa meter dijual untuk digantung di ruang kelas untuk tujuan pengajaran. [1]

Biasanya divisi menandai skala dengan ketepatan dua angka penting, dan pengguna memperkirakan angka ketiga. Beberapa slide rule kelas atas memiliki kursor pembesar yang membuat penandaan lebih mudah dilihat. Kursor semacam itu dapat secara efektif menggandakan akurasi pembacaan, memungkinkan slide rule 10 inci berfungsi sebaik 20 inci.

Berbagai kemudahan lainnya telah dikembangkan. Timbangan trigonometri kadang-kadang diberi label ganda, dalam warna hitam dan merah, dengan sudut-sudut yang saling melengkapi, yang disebut gaya "Darmstadt". Aturan geser dupleks sering menduplikasi beberapa skala di bagian belakang. Timbangan sering "dipisah" untuk mendapatkan akurasi yang lebih tinggi.

Aturan geser khusus diciptakan untuk berbagai bentuk teknik, bisnis dan perbankan. Ini sering kali memiliki perhitungan umum yang secara langsung diekspresikan sebagai timbangan khusus, misalnya perhitungan pinjaman, jumlah pembelian optimal, atau persamaan teknik tertentu. Misalnya, perusahaan Fisher Controls mendistribusikan slide rule khusus yang disesuaikan untuk memecahkan persamaan yang digunakan untuk memilih ukuran katup kontrol aliran industri yang tepat. ^[]

Aturan geser melingkar

Kaidah geser melingkar tersedia dalam dua jenis dasar, satu dengan dua kursor (kiri), dan satu lagi dengan piringan yang bisa digerakkan dan kursor tunggal (kanan). Versi kursor ganda melakukan perkalian dan pembagian dengan mempertahankan sudut tetap di antara kursor saat diputar di sekitar dial. Versi kursor tunggal beroperasi lebih seperti aturan geser standar melalui penyelarasan skala yang sesuai.

Keuntungan dasar dari aturan geser melingkar adalah bahwa dimensi terpanjang dari alat ini dikurangi dengan faktor sekitar 3 (yaitu, sebesar π). Misalnya, skala luar dari lingkaran 10 cm akan memiliki presisi maksimum yang sama dengan aturan geser biasa 30 cm. Aturan geser melingkar juga mengeliminasi kalkulasi "di luar skala", karena skalanya didesain untuk "membungkus"; mereka tidak pernah harus diorientasikan ulang ketika hasilnya mendekati 1,0-aturannya selalu pada skala. Namun demikian, untuk skala non-siklus non-spiral seperti S, T, dan LL, panjang skala diperpendek untuk memberi ruang bagi margin ujung.

Kaidah geser melingkar secara mekanis lebih kokoh dan bergerak lebih mulus, tetapi ketepatan penyelarasan skalanya sensitif terhadap pemusatan pivot pusat; satu menit 0,1 mm di luar pusat pivot bisa menghasilkan kesalahan penyelarasan terburuk 0,2 mm. Namun demikian, pivot mencegah goresan pada muka dan kursor. Skala akurasi tertinggi ditempatkan pada cincin luar. Alih-alih timbangan "split", circular rule kelas atas menggunakan timbangan spiral untuk operasi yang lebih kompleks seperti timbangan log-of-log. Satu circular rule premium delapan inci memiliki skala log-log spiral 50 inci.

Kerugian utama circular slide rules adalah kesulitan dalam menemukan angka di sepanjang piringan yang berputar, dan jumlah skala yang terbatas. Kelemahan lain dari slide rule melingkar adalah, bahwa skala yang kurang penting lebih dekat ke pusat, dan memiliki presisi yang lebih rendah. Sebagian besar siswa mempelajari penggunaan slide rule pada slide rule linear, dan tidak menemukan alasan untuk beralih.

Satu aturan geser yang masih digunakan sehari-hari di seluruh dunia adalah E6B. Ini adalah aturan geser melingkar yang pertama kali dibuat pada tahun 1930-an untuk pilot pesawat terbang untuk membantu perhitungan mati. Dengan bantuan skala yang tercetak pada bingkai, alat ini juga membantu dengan tugas-tugas lain seperti mengkonversi waktu, jarak, kecepatan, dan nilai suhu, kesalahan kompas, dan menghitung penggunaan bahan bakar. Apa yang disebut "roda doa" masih tersedia di toko-toko penerbangan, dan tetap digunakan secara luas. Sementara GPS telah mengurangi penggunaan perhitungan mati untuk navigasi udara, dan kalkulator genggam telah mengambil alih banyak fungsinya, E6B tetap digunakan secara luas sebagai perangkat utama atau cadangan, dan sebagian besar sekolah penerbangan menuntut agar siswanya memiliki beberapa tingkat penguasaannya.

Pada tahun 1952, perusahaan arloji Swiss, Breitling, memperkenalkan jam tangan pilot dengan aturan geser melingkar terintegrasi yang dikhususkan untuk perhitungan penerbangan: Breitling Navitimer. Aturan melingkar Navitimer, yang disebut oleh Breitling sebagai "komputer navigasi", menampilkan fungsi kecepatan udara, laju/waktu pendakian/penurunan, waktu penerbangan, jarak, dan konsumsi bahan bakar, serta fungsi konversi jumlah bahan bakar kilometer-nautical mile dan galon-liter.

Bahan

Secara tradisional slide rules terbuat dari kayu keras seperti mahoni atau boxwood dengan kursor dari kaca dan logam. Setidaknya satu instrumen presisi tinggi terbuat dari baja.

Pada tahun 1895, sebuah perusahaan Jepang, Hemmi, mulai membuat slide rules dari bambu, yang memiliki keunggulan stabil secara dimensi, kuat dan secara alami melumasi sendiri. Aturan geser bambu ini diperkenalkan di Swedia pada bulan September 1933 [2], dan mungkin hanya sedikit lebih awal di Jerman. Timbangan terbuat dari seluloid atau plastik. Kemudian slide rules terbuat dari plastik, atau aluminium yang dicat dengan plastik. Kursor selanjutnya adalah akrilik atau polikarbonat yang meluncur pada bantalan Teflon.

Semua slide rules premium memiliki angka dan skala yang diukir, dan kemudian diisi dengan cat atau resin lainnya. Aturan geser yang dicat atau dicetak dipandang lebih rendah karena penandaannya bisa luntur. Namun demikian, Pickett, mungkin perusahaan slide rule paling sukses di Amerika, membuat semua skala yang dicetak. Slide rule premium termasuk tangkapan pintar sehingga aturan tidak akan berantakan secara tidak sengaja, dan bumper untuk melindungi timbangan dan kursor dari gesekan di atas meja. Metode pembersihan yang direkomendasikan untuk tanda terukir adalah dengan menggosok ringan dengan steel-wool. Untuk kaidah geser yang dicat, dan bagi yang lemah hati, gunakan cairan pembersih jendela komersial yang diencerkan dan kain lembut.

Aturan geser melingkar Pickett dengan dua kursor. (Diameter 4,25 in./10,9 cm) Kebalikannya memiliki skala tambahan dan satu kursor.


Aturan geser melingkar sederhana, dibuat oleh Concise Co, Ltd, Tokyo, Jepang, hanya dengan skala terbalik, persegi dan kubik. Pada bagian belakangnya terdapat daftar 38 faktor konversi metrik/imperial yang praktis.


Jam tangan Breitling Navitimer dengan aturan geser melingkar

Sejarah

Aturan geser ditemukan sekitar tahun 1620-1630, tak lama setelah publikasi John Napier tentang konsep logaritma. Edmund Gunter dari Oxford mengembangkan perangkat penghitungan dengan skala logaritmik tunggal, yang, dengan alat ukur tambahan, dapat digunakan untuk mengalikan dan membagi. Deskripsi pertama dari skala ini diterbitkan di Paris pada tahun 1624 oleh Edmund Wingate (c. 1593 - 1656), seorang matematikawan Inggris, dalam sebuah buku berjudul "L'usage de la reigle de proportion en l'arithmetique & geometrie". Buku ini berisi skala ganda di satu sisi yang merupakan skala logaritmik dan di sisi lain skala tabular. Pada tahun 1630, William Oughtred dari Cambridge menemukan aturan slide melingkar, dan pada tahun 1632 ia menggabungkan dua aturan Gunter, yang dipegang bersama dengan tangan, untuk membuat perangkat yang dapat dikenali sebagai aturan slide modern. Seperti rekan sezamannya di Cambridge, Isaac Newton, Oughtred mengajarkan ide-idenya secara pribadi kepada murid-muridnya, tetapi tertunda dalam menerbitkannya, dan seperti Newton, ia terlibat dalam kontroversi yang sangat pedas mengenai prioritas, dengan muridnya yang satu kali, Richard Delamain, dan klaim sebelumnya dari Wingate. Gagasan Oughtred hanya dipublikasikan dalam publikasi muridnya William Forster pada tahun 1632 dan 1653.

Pada tahun 1677, Henry Coggeshall menciptakan aturan lipat dua kaki untuk mengukur kayu, yang disebut aturan geser Coggeshall. Desain dan kegunaannya untuk alat ini memberikan tujuan aturan geser di luar penyelidikan matematika.

Pada tahun 1722, Warner memperkenalkan skala dua dan tiga dekade, dan pada tahun 1755 Everard menyertakan skala terbalik; aturan geser yang berisi semua skala ini biasanya dikenal sebagai aturan "polifase".

Pada tahun 1815, Peter Roget menemukan log log slide rule, yang mencakup skala yang menampilkan logaritma dari logaritma. Hal ini memungkinkan pengguna untuk secara langsung melakukan perhitungan yang melibatkan akar dan eksponen. Ini sangat berguna untuk pangkat pecahan.

Bentuk modern

Bentuk yang lebih modern diciptakan pada tahun 1859 oleh letnan artileri Perancis, Amédée Mannheim, "yang beruntung karena aturannya dibuat oleh perusahaan dengan reputasi nasional dan diadopsi oleh Artileri Perancis." Sekitar waktu itu, karena teknik menjadi aktivitas profesional yang diakui, aturan geser mulai digunakan secara luas di Eropa. Mereka tidak menjadi umum di Amerika Serikat sampai tahun 1881, ketika Edwin Thacher memperkenalkan aturan silinder di sana. Aturan dupleks ditemukan oleh William Cox pada tahun 1891, dan diproduksi oleh Keuffel dan Esser Co. dari New York.

Pekerjaan astronomi juga membutuhkan perhitungan yang baik, dan pada abad ke-19 di Jerman, sebuah aturan geser baja sepanjang 2 meter digunakan di salah satu observatorium. Alat ini memiliki mikroskop yang terpasang, memberikan akurasi hingga enam tempat desimal.

Dalam Perang Dunia II, para bombardier dan navigator yang memerlukan perhitungan cepat, sering menggunakan slide rule khusus. Salah satu kantor Angkatan Laut AS sebenarnya merancang "sasis" aturan geser generik dengan bodi aluminium dan kursor plastik, di mana kartu seluloid (dicetak pada kedua sisinya) bisa ditempatkan untuk perhitungan khusus. Proses ini diciptakan untuk menghitung jangkauan, penggunaan bahan bakar dan ketinggian untuk pesawat terbang, dan kemudian diadaptasi untuk banyak tujuan lainnya.

Sepanjang tahun 1950-an dan 1960-an, aturan geser adalah simbol profesi insinyur (dengan cara yang sama seperti stetoskop melambangkan profesi medis).^[] Ilmuwan roket Jerman, Wernher von Braun, membawa dua slide rule Nestler antik tahun 1930-an bersamanya ketika dia pindah ke AS setelah Perang Dunia II untuk bekerja pada program luar angkasa Amerika. Sepanjang hidupnya, dia tidak pernah menggunakan alat hitung saku lainnya; aturan geser melayaninya dengan sangat baik untuk membuat estimasi cepat parameter desain roket dan angka-angka lainnya. Aturan geser merek Pickett aluminium dibawa pada lima misi ruang angkasa Apollo, termasuk ke bulan, menurut iklan pada kotak aturan geser N600 Pickett [3].

Beberapa mahasiswa teknik dan insinyur membawa slide rule sepuluh inci dalam sarung sabuk, dan bahkan sampai pertengahan tahun 1970-an, hal ini merupakan pemandangan umum di kampus-kampus. Para mahasiswa juga mungkin menyimpan aturan sepuluh atau dua puluh inci untuk pekerjaan presisi di rumah atau kantor sambil membawa aturan geser saku lima inci.

Pada tahun 2004, para peneliti pendidikan David B. Sher dan Dean C. Nataro menyusun jenis baru aturan geser berdasarkan prosthaphaeresis, sebuah algoritma untuk produk komputasi cepat yang mendahului logaritma. Namun, hanya ada sedikit minat praktis dalam membangunnya di luar prototipe awal. [4]

Penurunan

Pentingnya aturan geser mulai berkurang karena komputer elektronik, sumber daya baru tetapi sangat langka pada tahun 1950-an, menjadi tersedia secara luas bagi pekerja teknis selama tahun 1960-an. Pengenalan Fortran pada tahun 1957 membuat komputer menjadi praktis untuk memecahkan masalah matematika ukuran sederhana. IBM memperkenalkan serangkaian komputer yang lebih terjangkau, IBM 650 (1954), IBM 1620 (1959), IBM 1130 (1965) yang ditujukan kepada pasar sains dan teknik. Bahasa pemrograman BASIC John Kemeny (1964) memudahkan para siswa untuk menggunakan komputer. Komputer mini DEC PDP-8 diperkenalkan pada tahun 1965.

Komputer juga mengubah sifat perhitungan. Dengan aturan geser, ada penekanan besar pada pengerjaan aljabar untuk mendapatkan ekspresi ke dalam bentuk yang paling dapat dihitung. Pengguna aturan geser hanya akan memperkirakan atau menghilangkan istilah-istilah kecil untuk menyederhanakan perhitungan. Fortran memungkinkan rumus-rumus yang rumit untuk diketik dari buku teks tanpa upaya reformulasi. Integrasi numerik sering kali lebih mudah daripada mencoba menemukan solusi bentuk tertutup untuk masalah yang sulit. Insinyur muda yang meminta waktu komputer untuk memecahkan masalah yang bisa dilakukan dengan beberapa gesekan pada slide rule menjadi klise yang lucu. Banyak pusat komputer memiliki slide rule berbingkai yang digantung di dinding dengan catatan "Dalam keadaan darurat, pecahkan kaca."

Langkah lain menuju penggantian slide rules dengan elektronik adalah pengembangan kalkulator elektronik untuk penggunaan ilmiah dan teknik. Yang pertama termasuk Wang Laboratories LOCI-2, yang diperkenalkan pada tahun 1965, yang menggunakan logaritma untuk perkalian dan pembagian dan Hewlett-Packard HP-9100, yang diperkenalkan pada tahun 1968. HP-9100 memiliki fungsi trigonometri (sin, cos, tan) selain eksponensial dan logaritma. HP-9100 menggunakan algoritma CORDIC (coordinate rotation digital computer), yang memungkinkan perhitungan fungsi trigonometri hanya menggunakan operasi shift dan add. Metode ini memfasilitasi pengembangan kalkulator ilmiah yang semakin kecil.

Paku terakhir di peti mati untuk slide rule adalah peluncuran kalkulator ilmiah berukuran saku, di mana Hewlett-Packard HP-35 tahun 1972 adalah yang pertama. Kalkulator semacam itu dikenal sebagai kalkulator "slide rule" karena dapat melakukan sebagian besar atau semua fungsi pada slide rule. Dengan harga beberapa ratus dolar, bahkan kalkulator ini dianggap mahal bagi kebanyakan siswa. Sementara slide rule profesional juga bisa sangat mahal, toko obat sering menjual model plastik dasar dengan harga di bawah $ 20 USD. Tetapi pada tahun 1975, kalkulator elektronik empat fungsi dasar dapat dibeli dengan harga di bawah $50. Pada tahun 1976, TI-30 menawarkan kalkulator ilmiah dengan harga di bawah $25. Setelah waktu ini, pasar untuk slide rules mengering dengan cepat karena kalkulator ilmiah kecil menjadi terjangkau.

William Oughtred (1575-1660), penemu aturan geser melingkar


Insinyur menggunakan aturan geser. Perhatikan kalkulator mekanis di latar belakang.


TI-30

Keuntungan

• Aturan geser cenderung memoderasi kekeliruan "presisi palsu" dan signifikansi. Presisi tipikal yang tersedia bagi pengguna aturan geser adalah sekitar tiga tempat akurasi. Hal ini sesuai dengan sebagian besar data yang tersedia untuk input ke rumus teknik. Ketika kalkulator saku modern digunakan, ketepatannya dapat ditampilkan hingga tujuh tempat desimal atau lebih, sementara pada kenyataannya hasilnya tidak pernah bisa lebih akurat daripada data input yang tersedia.
• Aturan geser memerlukan estimasi terus-menerus dari urutan besarnya hasil. Pada slide rule 1,5 × 30 (yang sama dengan 45) akan menunjukkan hasil yang sama dengan 1.500.000 × 0,03 (yang sama dengan 45.000). Terserah pada insinyur untuk terus menentukan kewajaran hasil, sesuatu yang bisa hilang ketika angka-angka dimasukkan secara sembarangan ke dalam program komputer atau kalkulator.
• Ketika melakukan urutan perkalian atau pembagian dengan angka yang sama, jawabannya sering kali dapat ditentukan hanya dengan melirik ke arah slide rule tanpa manipulasi apa pun. Hal ini bisa sangat berguna apabila menghitung persentase, misalnya, untuk nilai tes, atau ketika membandingkan harga, misalnya, dalam dolar per kilogram. Beberapa perhitungan kecepatan-waktu-jarak dapat dilakukan secara hands-free dalam sekejap dengan slide rule.
• Aturan geser tidak bergantung pada listrik.
• Aturan geser adalah teknologi yang mudah direplikasi. Dari contoh slide rule yang diberikan, lebih banyak lagi yang dapat dibuat oleh pengrajin yang kompeten dari bahan yang belum sempurna dengan menggunakan proses non-industri.
• Slide rules sangat terstandardisasi, jadi tidak perlu mempelajari ulang apa pun apabila beralih ke aturan yang berbeda.
• Aturan geser serbaguna, dan bisa dioperasikan dalam situasi dan lingkungan di mana pengguna manusia mungkin memiliki ketangkasan yang berkurang (misalnya, karena membutuhkan sarung tangan pelindung). Sebaliknya, kalkulator bisa sulit dioperasikan dalam situasi seperti itu - aturan geser tidak mungkin menghasilkan kesalahan yang serupa dengan kesalahan yang diakibatkan oleh salah menekan tombol yang salah pada kalkulator.
• Aturan geser bisa dibuat dari karton atau kertas. Banyak bagan gratis atau alat penghitung khusus yang terbuat dari karton yang sebenarnya adalah aturan geser linier atau melingkar khusus.

Salah satu keuntungan menggunakan slide rule bersama dengan kalkulator elektronik adalah bahwa perhitungan penting dapat diperiksa dengan melakukannya pada keduanya; karena kedua instrumen tersebut sangat berbeda, kecil kemungkinannya untuk membuat kesalahan yang sama dua kali.

Kekurangan

• Kesalahan bisa timbul dari ketidaktepatan mekanis.
• Perhitungan menggunakan aturan geser memiliki presisi terbatas karena input dan output analognya. Sebaliknya, karena input numerik diskrit dan operasi elektronik floating point, bahkan kalkulator modern yang sederhana pun memiliki resolusi output setidaknya enam angka penting.

Halaman terkait

• Abacus
• Logaritma