Fungsi eksponensial
Dalam matematika, fungsi eksponensial adalah fungsi yang tumbuh dengan cepat. Lebih tepatnya, itu adalah fungsi exp ( x ) = e x {\displaystyle \exp(x)=e^{x}}} 
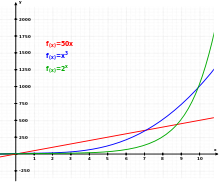
Tiga fungsi yang berbeda: Linear (merah), Kubik (biru) dan Eksponensial (hijau).
Properti
Karena fungsi eksponensial menggunakan eksponensial, maka fungsi-fungsi ini mengikuti aturan yang sama. Dengan demikian,
exp ( x + y ) = exp ( x ) exp ( y ) = e x + y {\displaystyle \exp(x+y)=\exp(x)\exp(y)=e^{x+y}} 

Logaritma natural adalah operasi kebalikan dari fungsi eksponensial.
ln ( x ) = log e ( x ) = log ( x ) log ( e ) {\displaystyle \ln(x)=\log _{e}(x)={\frac {\log(x)}{\log(e)}}}}
Fungsi eksponensial memenuhi properti yang menarik dan penting dalam kalkulus diferensial,
d d x e x = e x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}} 
Ini berarti bahwa kemiringan fungsi eksponensial adalah fungsi eksponensial itu sendiri, dan selanjutnya ini berarti memiliki kemiringan 1 pada x = 0 {\displaystyle x=0}
Aplikasi
Fungsi eksponensial adalah salah satu fungsi matematika yang paling berguna. Fungsi ini digunakan untuk merepresentasikan pertumbuhan eksponensial, yang memiliki kegunaan di hampir semua mata pelajaran sains dan juga menonjol di bidang Keuangan. Peluruhan eksponensial juga terjadi, misalnya peluruhan radioaktif dan penyerapan cahaya.
Salah satu contoh fungsi eksponensial dalam kehidupan nyata adalah bunga di bank. Jika seseorang mendepositokan £100 ke dalam rekening yang mendapat bunga 3% per bulan, maka saldo setiap bulannya adalah (dengan asumsi uang tidak tersentuh):
| Bulan | Keseimbangan | Bulan | Keseimbangan |
| Januari | £100.00 | Juli | £119.41 |
| Februari | £103.00 | Agustus | £122.99 |
| Maret | £106.09 | September | £126.68 |
| April | £109.27 | Oktober | £130.48 |
| Mei | £112.55 | November | £134.39 |
| Juni | £115.93 | Desember | £138.42 |
Perhatikan bagaimana uang tambahan dari bunga meningkat setiap bulan. Semakin besar saldo awal, semakin banyak bunga yang akan didapat orang tersebut.
Dua contoh matematis dari fungsi eksponensial ditunjukkan di bawah ini.
| a=2
| a=3
|
Hubungan dengan konstanta matematika e
Meskipun basis ( a {\displaystyle a}
Angka e penting untuk setiap fungsi eksponensial. Misalnya, sebuah bank membayar bunga 0,01 persen setiap hari. Seseorang mengambil uang bunganya dan memasukkannya ke dalam sebuah kotak. Setelah 10.000 hari (sekitar 30 tahun), dia memiliki uang 2 kali lebih banyak daripada saat dia memulainya. Orang lain mengambil uang bunganya dan memasukkannya kembali ke bank. Karena bank sekarang membayar bunga atas bunganya, jumlah uangnya adalah fungsi eksponensial. Setelah 10.000 hari, dia tidak memiliki uang 2 kali lebih banyak dari yang dia mulai, tetapi dia memiliki uang 2,718145 kali lebih banyak dari yang dia mulai. Angka ini sangat dekat dengan angka e. Jika bank membayar bunga lebih sering, sehingga jumlah yang dibayarkan setiap kali lebih sedikit, maka angkanya akan lebih dekat dengan angka e.
Seseorang juga dapat melihat gambar untuk melihat mengapa angka e penting untuk fungsi eksponensial. Gambar tersebut memiliki tiga kurva yang berbeda. Kurva dengan titik-titik hitam adalah fungsi eksponensial dengan basis sedikit lebih kecil dari e. Kurva dengan garis hitam pendek adalah fungsi eksponensial dengan basis sedikit lebih besar dari e. Kurva biru adalah fungsi eksponensial dengan basis yang persis sama dengan e. Garis merah adalah garis singgung ke kurva biru. Garis merah menyentuh kurva biru pada satu titik tanpa melintasinya. Seseorang dapat melihat bahwa kurva merah melintasi sumbu x, garis yang bergerak dari kiri ke kanan, pada -1. Ini benar hanya untuk kurva biru. Inilah alasan mengapa fungsi eksponensial dengan basis e adalah spesial.
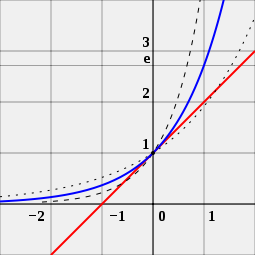
e adalah bilangan a yang unik, sehingga nilai turunan fungsi eksponensial f (x) = ax (kurva biru) pada titik x = 0 adalah tepat 1. Sebagai perbandingan, fungsi 2x (kurva putus-putus) dan 4x (kurva putus-putus) diperlihatkan; fungsi-fungsi ini tidak bersinggungan dengan garis kemiringan 1 (merah).
Pertanyaan dan Jawaban
T: Apa itu fungsi eksponensial?
J: Fungsi eksponensial adalah fungsi matematika yang tumbuh semakin cepat.
T: Bagaimana fungsi eksponensial diekspresikan secara matematis?
J: Fungsi eksponensial dinyatakan secara matematis sebagai exp(x) = e^x, di mana e adalah konstanta Euler.
T: Apa yang diwakili oleh konstanta Euler?
J: Konstanta Euler mewakili bilangan irasional yang kira-kira 2.71828.
T: Apakah fungsi eksponensial selalu meningkat?
J: Ya, fungsi eksponensial selalu meningkat nilainya seiring dengan meningkatnya x.
T: Apakah ada batasan seberapa cepat fungsi eksponensial dapat tumbuh?
J: Tidak, tidak ada batasan seberapa cepat fungsi eksponensial dapat tumbuh karena fungsi ini terus meningkat dengan nilai x yang lebih besar.
T: Bagaimana kita bisa menghitung konstanta Euler?
J: Kita dapat menghitung konstanta Euler dengan menggunakan metode numerik seperti deret Taylor atau pecahan lanjutan.
T: Apa aplikasi lain yang ada untuk fungsi eksponensial selain matematika?
J: Fungsi eksponensial memiliki banyak aplikasi di luar matematika termasuk fisika, kimia, biologi, ekonomi dan teknik.
Cari di dalam ensiklopedia

