Deret harmonik (matematika)

Dalam matematika, deret harmonik adalah deret tak hingga divergen:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}}{2}}}+{\frac {1}{3}}}+{\frac {1}{{4}}}+{\frac {1}{5}}}+\cdots } {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots }

Divergen berarti bahwa ketika Anda menambahkan lebih banyak suku, jumlahnya tidak pernah berhenti menjadi lebih besar. Itu tidak menuju ke satu nilai terbatas.

Tak terhingga berarti Anda selalu dapat menambahkan suku lain. Tidak ada suku terakhir untuk deret tersebut.

Namanya berasal dari ide harmonik dalam musik: panjang gelombang nada-nada dari senar yang bergetar adalah 1/2, 1/3, 1/4, dst., dari panjang gelombang dasar senar. Terlepas dari suku pertama, setiap suku dari deret adalah rata-rata harmonik dari suku-suku di kedua sisinya. Frasa rata-rata harmonik juga berasal dari musik.

Sejarah

Fakta bahwa deret harmonik menyimpang pertama kali dibuktikan pada abad ke-14 oleh Nicole Oresme, tetapi dilupakan. Bukti diberikan pada abad ke-17 oleh Pietro Mengoli, Johann Bernoulli, dan Jacob Bernoulli.

Urutan harmonis telah digunakan oleh para arsitek. Pada periode Barok, para arsitek menggunakannya dalam proporsi denah lantai, elevasi, dan dalam hubungan antara detail arsitektur gereja dan istana.

Divergensi

Ada beberapa bukti yang terkenal dari divergensi deret harmonik. Beberapa di antaranya diberikan di bawah ini.

Uji perbandingan

Salah satu cara untuk membuktikan divergensi adalah dengan membandingkan deret harmonik dengan deret divergen lainnya, di mana setiap penyebut diganti dengan pangkat dua terbesar berikutnya:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}}+{\frac {1}{3}}}+{\frac {1}{4}}+{\frac {1}{5}}}+{\frac {1}{6}}}+{\frac {1}{7}}}+{\frac {1}{{8}}+{\frac {1}{9}}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}}+{\frac {1}{\color {red}{\mathbf {4}} }}}+{\frac {1}{4}}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{\color {merah}{\mathbf {8}} }}}+{\frac {1}{\color {merah}{\mathbf {8}} }}}+{\frac {1}{{8}}+{\frac {1}{\color {red}{\mathbf {16}} }}}}+\cdots \end{aligned}}} {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}}

Setiap suku dari deret harmonik lebih besar daripada atau sama dengan suku yang bersesuaian dari deret kedua, dan oleh karena itu jumlah deret harmonik harus lebih besar daripada atau sama dengan jumlah deret kedua. Namun, jumlah deret kedua adalah tak terhingga:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\kiri({\frac {1}{{2}}}\right)+\kiri({\frac {1}{{4}}}\!+\!{\frac {1}{{4}}}\right)+\kiri({\frac {1}{8}}}\!+\!{\frac {1}{{8}}}\!+\!{\frac {1}{{8}}}\!+\!{\frac {1}{8}}}\right)+\kiri({\frac {1}{16}}}}\!+\!\cdots \!+\!!{\frac {1}{{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}}+{\frac {1}{{2}}}+{\frac {1}{{2}}}+{\frac {1}{2}}}+\cdots =\infty \end{aligned}}}} {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}}

Ini mengikuti (dengan uji perbandingan) bahwa jumlah deret harmonik haruslah tak hingga juga. Lebih tepatnya, perbandingan di atas membuktikan bahwa

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{{n}}\geq 1+{\frac {k}{2}}}} {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}}

untuk setiap bilangan bulat positif k.

Bukti ini, yang diusulkan oleh Nicole Oresme pada sekitar tahun 1350, dianggap sebagai titik tertinggi dari matematika abad pertengahan. Bukti ini masih merupakan bukti standar yang diajarkan di kelas-kelas matematika saat ini.

Tes integral

Adalah mungkin untuk membuktikan bahwa deret harmonik menyimpang dengan membandingkan jumlahnya dengan integral tak wajar. Perhatikan susunan persegi panjang yang ditunjukkan pada gambar di sebelah kanan. Setiap persegi panjang memiliki lebar 1 unit dan tinggi 1/n unit, sehingga total area dari jumlah persegi panjang yang tak terhingga adalah jumlah deret harmonik:

luas persegi panjang = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}}+{\frac {1}{3}}}+{\frac {1}{4}}}+{\frac {1}{5}}+\cdots } {\displaystyle {\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots }

Total area di bawah kurva y = 1/x dari 1 sampai tak terhingga diberikan oleh integral tak wajar yang divergen:

area di bawah kurva = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{\text{area under}}\\{\text{area under}}\\{\text{curve}}\\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}}\,dx=\infty . } {\displaystyle {\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .}

Karena area ini seluruhnya terkandung di dalam persegi panjang, maka total area persegi panjang haruslah tak terhingga juga. Ini membuktikan bahwa

∑ n = 1 k 1 n > ∫ 1 k + 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{{n}}>\int _{1}^{k+1}{\frac {1}{{x}}\,dx=\ln(k+1). } {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).}

Generalisasi dari argumen ini dikenal sebagai uji integral.

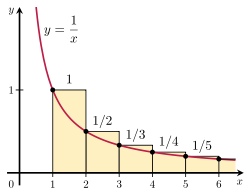
Ilustrasi uji integral.Zoom
Ilustrasi uji integral.

Tingkat divergensi

Deret harmonik menyimpang sangat lambat. Misalnya, jumlah dari 1043 suku pertama kurang dari 100. Ini karena jumlah parsial dari deret ini memiliki pertumbuhan logaritmik. Khususnya,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1} {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1}

dimana γ adalah konstanta Euler-Mascheroni dan εk ~ 1/2k yang mendekati 0 ketika k menuju tak terhingga. Leonhard Euler membuktikan hal ini dan juga bahwa penjumlahan yang hanya mencakup resiprokal dari bilangan prima juga divergen, yaitu:

∑ p prima 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}}+{\frac {1}{3}}}+{\frac {1}{5}}}+{\frac {1}{7}}}+{\frac {1}{11}}+{\frac {1}{{13}}}+{\frac {1}{{17}}+\cdots =\infty . } {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .}

Jumlah parsial

Tiga puluh angka harmonik pertama

n

Jumlah parsial dari deret harmonik, H n

 

dinyatakan sebagai pecahan

desimal

ukuran relatif

 

1

1

~1

1

 

 

2

3

/2

~1.5

1.5

 

 

3

11

/6

~1.83333

1.83333

 

 

4

25

/12

~2.08333

2.08333

 

 

5

137

/60

~2.28333

2.28333

 

 

6

49

/20

~2.45

2.45

 

 

7

363

/140

~2.59286

2.59286

 

 

8

761

/280

~2.71786

2.71786

 

 

9

7129

/2520

~2.82897

2.82897

 

 

10

7381

/2520

~2.92897

2.92897

 

 

11

83711

/27720

~3.01988

3.01988

 

 

12

86021

/27720

~3.10321

3.10321

 

 

13

1145993

/360360

~3.18013

3.18013

 

 

14

1171733

/360360

~3.25156

3.25156

 

 

15

1195757

/360360

~3.31823

3.31823

 

 

16

2436559

/720720

~3.38073

3.38073

 

 

17

42142223

/12252240

~3.43955

3.43955

 

 

18

14274301

/4084080

~3.49511

3.49511

 

 

19

275295799

/77597520

~3.54774

3.54774

 

 

20

55835135

/15519504

~3.59774

3.59774

 

 

21

18858053

/5173168

~3.64536

3.64536

 

 

22

19093197

/5173168

~3.69081

3.69081

 

 

23

444316699

/118982864

~3.73429

3.73429

 

 

24

1347822955

/356948592

~3.77596

3.77596

 

 

25

34052522467

/8923714800

~3.81596

3.81596

 

 

26

34395742267

/8923714800

~3.85442

3.85442

 

 

27

312536252003

/80313433200

~3.89146

3.89146

 

 

28

315404588903

/80313433200

~3.92717

3.92717

 

 

29

9227046511387

/2329089562800

~3.96165

3.96165

 

 

30

9304682830147

/2329089562800

~3.99499

3.99499

 

 

Jumlah parsial terbatas dari deret harmonik divergen,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},} {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},}

disebut bilangan harmonik.

Perbedaan antara Hn dan ln n konvergen ke konstanta Euler-Mascheroni. Selisih antara dua bilangan harmonik tidak pernah merupakan bilangan bulat. Tidak ada bilangan harmonik yang merupakan bilangan bulat, kecuali untuk H1 = 1.

Seri terkait

Rangkaian harmonik bolak-balik

Serial ini

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}}+{\frac {1}{3}}-{\frac {1}{4}}}+{\frac {1}{5}}-\cdots } {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots }

dikenal sebagai deret harmonik bolak-balik. Deret ini konvergen dengan uji deret bolak-balik. Khususnya, jumlahnya sama dengan logaritma natural dari 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}}+{\frac {1}{{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.} {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.}

Deret harmonik bolak-balik, meskipun konvergen bersyarat, tidak mutlak konvergen: jika suku-suku dalam deret diatur ulang secara sistematis, secara umum jumlahnya menjadi berbeda dan, bergantung pada pengaturan ulang, bahkan mungkin tak terbatas.

Rumus deret harmonik bolak-balik adalah kasus khusus dari deret Mercator, deret Taylor untuk logaritma natural.

Deret yang terkait dapat diturunkan dari deret Taylor untuk arctangent:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}}=1-{\frac {1}{{3}}+{\frac {1}{{5}}-{\frac {1}{7}}}+\cdots ={\frac {\pi }{4}}}. } {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.}

Ini dikenal sebagai deret Leibniz.

Rangkaian harmonik umum

Deret harmonik umum adalah dalam bentuk

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},} {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},}

dimana a ≠ 0 dan b adalah bilangan real, dan b/a bukan nol atau bilangan bulat negatif.

Dengan uji perbandingan batas dengan deret harmonik, semua deret harmonik umum juga divergen.

p-series

Sebuah generalisasi dari deret harmonik adalah deret-p (atau deret hiperharmonik), didefinisikan sebagai

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}} {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}}

untuk sembarang bilangan real p. Ketika p = 1, deret-p adalah deret harmonik, yang divergen. Baik uji integral atau uji kondensasi Cauchy menunjukkan bahwa deret-p konvergen untuk semua p > 1 (dalam hal ini disebut deret over-harmonik) dan divergen untuk semua p ≤ 1. Jika p > 1 maka jumlah dari deret-p adalah ζ(p), yaitu fungsi zeta Riemann yang dievaluasi pada p.

Masalah menemukan jumlah untuk p = 2 disebut masalah Basel; Leonhard Euler menunjukkan bahwa jumlahnya adalah π2 /6. Nilai dari penjumlahan untuk p = 3 disebut konstanta Apéry, karena Roger Apéry membuktikan bahwa itu adalah bilangan irasional.

ln-series

Terkait dengan deret-p adalah deret-ln, didefinisikan sebagai

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}} {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}}

untuk setiap bilangan real positif p. Hal ini dapat ditunjukkan dengan uji integral untuk divergen untuk p ≤ 1 tetapi konvergen untuk semua p > 1.

φ-series

Untuk setiap fungsi cembung bernilai real φ sedemikian rupa sehingga

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \kiri({\frac {u}{2}}}\kanan)}{\varphi (u)}}<{\frac {1}{2}}},} {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},}

seri

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}}\right)} {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)}

adalah konvergen. []

Deret harmonik acak

Deret harmonik acak

∑ n = 1 ∞ s n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},} {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},}

dimana sn adalah variabel acak independen yang terdistribusi secara identik yang mengambil nilai +1 dan -1 dengan probabilitas yang sama 1/2, adalah contoh yang terkenal dalam teori probabilitas untuk serangkaian variabel acak yang konvergen dengan probabilitas 1. Fakta konvergensi ini merupakan konsekuensi mudah dari teorema tiga seri Kolmogorov atau dari ketidaksetaraan maksimal Kolmogorov yang terkait erat. Byron Schmuland dari Universitas Alberta meneliti lebih lanjut sifat-sifat deret harmonik acak, dan menunjukkan bahwa deret konvergen adalah variabel acak dengan beberapa sifat yang menarik. −42 Makalah Schmuland menjelaskan mengapa probabilitas ini begitu dekat dengan, tetapi tidak persis 1/8. Nilai pasti dari probabilitas ini diberikan oleh integral produk kosinus tak hingga C2 dibagi dengan π.

Rangkaian harmonik yang habis

Deret harmonik yang habis dimana semua suku dimana digit 9 muncul dimanapun dalam penyebutnya dihilangkan dapat ditunjukkan untuk konvergen dan nilainya kurang dari 80. Pada kenyataannya, ketika semua suku yang mengandung deretan digit tertentu (dalam basis apapun) dihilangkan, deret ini akan konvergen.

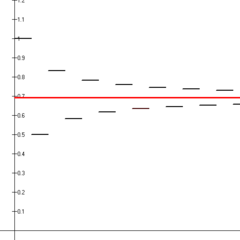
Empat belas jumlah parsial pertama dari deret harmonik bolak-balik (segmen garis hitam) yang ditunjukkan konvergen ke logaritma natural 2 (garis merah).Zoom
Empat belas jumlah parsial pertama dari deret harmonik bolak-balik (segmen garis hitam) yang ditunjukkan konvergen ke logaritma natural 2 (garis merah).

Aplikasi

Deret harmonik bisa berlawanan dengan intuisi. Ini karena deret harmonik adalah deret divergen meskipun suku-suku deret semakin kecil dan menuju nol. Divergensi deret harmonik adalah sumber dari beberapa paradoks.

  • "Cacing pada karet gelang". Misalkan seekor cacing merangkak di sepanjang karet gelang satu meter yang elastis tak terhingga pada saat yang sama ketika karet gelang diregangkan secara seragam. Jika cacing berjalan 1 sentimeter per menit dan karet gelang meregang 1 meter per menit, apakah cacing akan mencapai ujung karet gelang? Jawabannya, secara berlawanan dengan intuisi, adalah "ya", karena setelah n menit, rasio jarak yang ditempuh oleh cacing terhadap total panjang karet gelang adalah

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}}\sum _{k=1}^{n}{\frac {1}{k}}. } {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.}

Karena deret ini menjadi besar secara arbitrer ketika n menjadi lebih besar, pada akhirnya rasio ini harus melebihi 1, yang menyiratkan bahwa cacing mencapai ujung karet gelang. Namun demikian, nilai n di mana hal ini terjadi haruslah sangat besar: kira-kira e100 , suatu angka yang melebihi 1043 menit (1037 tahun). Walaupun deret harmonik memang menyimpang, namun hal itu terjadi sangat lambat.

  • Masalah Jeep menanyakan berapa banyak total bahan bakar yang diperlukan untuk sebuah mobil dengan kapasitas pembawa bahan bakar terbatas untuk melintasi gurun pasir yang meninggalkan tetesan bahan bakar di sepanjang rute. Jarak yang bisa ditempuh mobil dengan jumlah bahan bakar tertentu terkait dengan jumlah parsial dari deret harmonik, yang tumbuh secara logaritmik. Dan bahan bakar yang dibutuhkan meningkat secara eksponensial dengan jarak yang diinginkan.
  • Masalah penumpukan balok: diberikan kumpulan kartu domino yang identik, adalah mungkin untuk menumpuknya di tepi meja sehingga kartu-kartu tersebut menggantung di tepi meja tanpa jatuh. Hasil yang berlawanan dengan intuisi adalah bahwa mereka dapat ditumpuk dengan cara yang membuat overhang sebesar yang Anda inginkan. Artinya, asalkan ada cukup banyak kartu domino.
  • Seorang perenang yang melaju lebih cepat setiap kali mereka menyentuh dinding kolam. Perenang mulai menyeberangi kolam 10 meter dengan kecepatan 2 m/detik, dan setiap kali menyeberangi kolam, 2 m/detik lagi ditambahkan ke kecepatannya. Secara teori, kecepatan perenang tidak terbatas, tetapi jumlah penyeberangan kolam yang diperlukan untuk mencapai kecepatan itu menjadi sangat besar; misalnya, untuk mencapai kecepatan cahaya (mengabaikan relativitas khusus), perenang perlu menyeberangi kolam 150 juta kali. Berlawanan dengan angka yang besar ini, waktu yang dibutuhkan untuk mencapai kecepatan tertentu bergantung pada jumlah seri pada sejumlah persilangan kolam yang diberikan:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{{2}}}\sum _{k=1}^{n}{\frac {1}{k}}. } {\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.}

Menghitung jumlah menunjukkan bahwa waktu yang diperlukan untuk mencapai kecepatan cahaya hanya 97 detik.

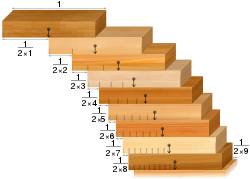
Masalah penumpukan-blok: blok-blok yang disejajarkan menurut deret harmonik menjembatani belahan-belahan dengan lebar berapa pun.Zoom
Masalah penumpukan-blok: blok-blok yang disejajarkan menurut deret harmonik menjembatani belahan-belahan dengan lebar berapa pun.

Halaman terkait

  • Perkembangan harmonis
  • Daftar jumlah resiprokal

Pertanyaan dan Jawaban

T: Apa yang dimaksud dengan deret harmonik?


J: Deret harmonik adalah deret divergen tak terbatas di mana setiap suku sama dengan 1 dibagi dengan posisinya dalam deret tersebut.

T: Apa yang dimaksud dengan deret divergen?


J: Divergen berarti bahwa ketika Anda menambahkan lebih banyak suku, jumlahnya tidak pernah berhenti menjadi lebih besar dan tidak menuju ke satu nilai terbatas.

T: Apa yang dimaksud dengan deret tak hingga?


J: Tak terhingga berarti bahwa Anda selalu dapat menambahkan suku lain dan tidak ada suku terakhir pada deret tersebut.

T: Dari mana nama deret ini berasal?


J: Nama deret ini berasal dari ide harmonik dalam musik, di mana panjang gelombang nada-nada adalah 1/2, 1/3, 1/4, dst., dari panjang gelombang fundamental senar.

T: Apa yang dimaksud dengan arti harmonik?


J: Rerata harmonik adalah ketika setiap suku dalam suatu deret sama dengan rerata harmonik dari suku-suku tetangganya. Frasa ini juga berasal dari musik.

T: Bagaimana kita menghitung setiap suku dalam deret ini?


J: Setiap suku dalam deret ini dapat dihitung dengan membagi satu dengan posisinya dalam deret (1/n).

AlegsaOnline.com - 2020 / 2023 - License CC3