Transformasi Fourier

Transformasi Fourier adalah fungsi matematika yang dapat digunakan untuk menemukan frekuensi dasar yang membentuk sinyal atau gelombang. Misalnya, jika sebuah akor dimainkan, gelombang suara akor dapat dimasukkan ke dalam transformasi Fourier untuk menemukan nada-nada yang membentuk akor tersebut. Output dari transformasi Fourier kadang-kadang disebut spektrum atau distribusi frekuensi karena menampilkan spektrum frekuensi input. Fungsi ini memiliki banyak kegunaan dalam kriptografi, oseanografi, pembelajaran mesin, radiologi, fisika kuantum serta desain dan visualisasi suara.

Transformasi Fourier dari fungsi f ( x ) {\displaystyle f(x)} f(x) diberikan oleh

F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\displaystyle F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx} $F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx$

α {\displaystyle \alpha } $\alpha$ adalah frekuensi

F ( α ) {\displaystyle F(\alpha )} $F(\alpha )$ adalah fungsi transformasi Fourier dan mengembalikan nilai yang mewakili seberapa lazim frekuensi α {\displaystyle \alpha } $\alpha$ dalam sinyal asli.

e - 2 π i α x {\displaystyle e^{-2\pi i\alpha x}} $e^{-2\pi i\alpha x}$ Merupakan pembungkus fungsi input f ( x ) {\displaystyle f(x)} f(x) di sekitar titik asal dalam bidang kompleks pada beberapa frekuensi α {\displaystyle \alpha } $\alpha$

Transformasi Fourier terbalik diberikan oleh

f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {\displaystyle f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha } $f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha$

Transformasi Fourier menunjukkan frekuensi apa yang ada dalam sinyal. Misalnya, perhatikan gelombang suara yang mengandung tiga nada musik yang berbeda: A, B, dan C. Membuat grafik transformasi Fourier dari gelombang suara ini (dengan frekuensi pada sumbu x dan intensitas pada sumbu y) akan menunjukkan puncak pada setiap frekuensi yang sesuai dengan salah satu nada musik.

Banyak sinyal dapat dibuat dengan menambahkan bersama kosinus dan sinus dengan amplitudo dan frekuensi yang bervariasi. Transformasi Fourier memplot amplitudo dan fase dari kosinus dan sinus ini terhadap frekuensi masing-masing.

Transformasi Fourier penting karena banyak sinyal yang lebih masuk akal ketika frekuensinya dipisahkan. Dalam contoh audio di atas, melihat sinyal sehubungan dengan waktu tidak memperjelas bahwa nada A, B, dan C ada dalam sinyal. Banyak sistem yang melakukan hal yang berbeda pada frekuensi yang berbeda, sehingga sistem semacam ini dapat dijelaskan oleh apa yang mereka lakukan pada setiap frekuensi. Contoh dari hal ini adalah filter yang memblokir frekuensi tinggi.

Menghitung transformasi Fourier memerlukan pemahaman tentang integrasi dan bilangan imajiner. Komputer biasanya digunakan untuk menghitung transformasi Fourier dari apa pun kecuali sinyal yang paling sederhana. Fast Fourier Transform adalah metode yang digunakan komputer untuk menghitung transformasi Fourier dengan cepat.

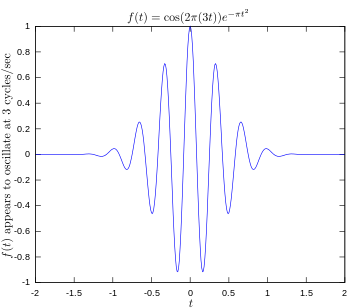
Fungsi asli menunjukkan sinyal yang berosilasi pada 3 hertz.

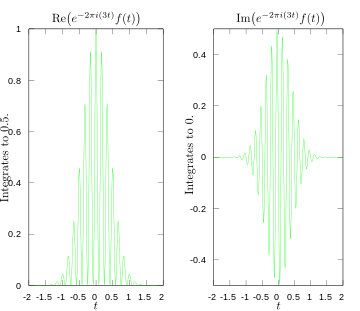
Bagian nyata dan imajiner dari integrand untuk transformasi Fourier pada 3 hertz

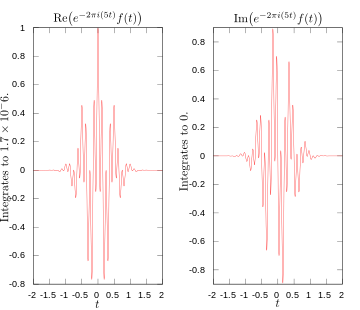
Bagian nyata dan imajiner dari integrand untuk transformasi Fourier pada 5 hertz

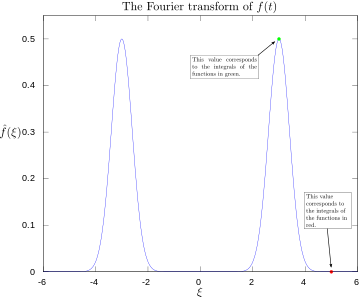
Transformasi Fourier dengan label 3 dan 5 hertz.

Pertanyaan dan Jawaban

T: Apa yang dimaksud dengan transformasi Fourier?

J: Transformasi Fourier adalah fungsi matematis yang dapat digunakan untuk menemukan frekuensi dasar dari sebuah gelombang. Fungsi ini mengambil gelombang kompleks dan menemukan frekuensi-frekuensi yang membentuknya, sehingga memungkinkannya untuk mengidentifikasi nada-nada yang membentuk sebuah akor.

T: Apa saja kegunaan transformasi Fourier?

J: Transformasi Fourier memiliki banyak kegunaan dalam kriptografi, oseanografi, pembelajaran mesin, radiologi, fisika kuantum serta desain dan visualisasi suara.

T: Bagaimana transformasi Fourier dihitung?

J: Transformasi Fourier dari fungsi f(x) diberikan oleh F(ב) = ∫-∞+∞f(x)e-2נiבxdx di mana ב adalah frekuensi. Ini mengembalikan nilai yang mewakili seberapa lazim frekuensi ב dalam sinyal asli. Transformasi Fourier terbalik diberikan oleh f(x) = ∫-∞+∞F(ב)e+2נixבdב.

T: Seperti apa output dari Transformasi Fourier?

J: Keluaran dari Transformasi Fourier dapat disebut spektrum atau distribusi frekuensi karena menampilkan distribusi frekuensi yang mungkin dari input.

T: Bagaimana komputer menghitung Transformasi Fourier Cepat?

J: Komputer menggunakan algoritma yang disebut Transformasi Fourier Cepat (FFT) untuk menghitung dengan cepat, kecuali transformasi sinyal yang paling sederhana.

T: Apa yang tidak ditunjukkan oleh melihat sinyal terhadap waktu?

J: Melihat sinyal sehubungan dengan waktu tidak memperjelas nada-nada apa yang ada di dalamnya; banyak sinyal yang lebih masuk akal ketika frekuensinya dipisahkan dan dianalisis satu per satu.