Tegangan permukaan

Penyebab

Gaya kohesif di antara molekul cairan menyebabkan tegangan permukaan. Dalam sebagian besar cairan, setiap molekul ditarik sama rata ke segala arah oleh molekul cairan di sekitarnya, sehingga menghasilkan gaya bersih nol. Molekul-molekul di permukaan tidak memiliki molekul lain di semua sisinya dan oleh karena itu ditarik ke dalam. Hal ini menciptakan beberapa tekanan internal dan memaksa permukaan cairan untuk berkontraksi ke area minimal.

Tegangan permukaan bertanggung jawab atas bentuk tetesan cairan. Meskipun mudah berubah bentuk, tetesan air cenderung ditarik ke dalam bentuk bola oleh gaya kohesif lapisan permukaan. Dengan tidak adanya gaya lain, termasuk gravitasi, tetesan hampir semua cairan akan berbentuk bulat sempurna. Bentuk bola meminimalkan "tegangan dinding" yang diperlukan dari lapisan permukaan menurut hukum Laplace.

Cara lain untuk melihatnya adalah dalam hal energi. Sebuah molekul yang bersentuhan dengan tetangga berada dalam keadaan energi yang lebih rendah daripada jika ia sendirian (tidak bersentuhan dengan tetangga). Molekul interior memiliki tetangga sebanyak yang mereka bisa miliki, tetapi molekul batas tidak memiliki tetangga (dibandingkan dengan molekul interior). Jadi, molekul-molekul batas memiliki energi yang lebih tinggi. Agar cairan meminimalkan keadaan energinya, jumlah molekul batas yang berenergi lebih tinggi harus diminimalkan. Jumlah molekul batas yang diminimalkan menghasilkan area permukaan yang diminimalkan.

Sebagai hasil dari minimalisasi luas permukaan, sebuah permukaan akan mengasumsikan bentuk yang paling halus yang bisa dilakukannya. Setiap kelengkungan dalam bentuk permukaan menghasilkan area yang lebih besar dan energi yang lebih tinggi. Jadi, permukaan akan mendorong kembali terhadap kelengkungan apa pun dengan cara yang sama seperti bola yang didorong ke atas bukit akan mendorong kembali untuk meminimalkan energi potensial gravitasinya.

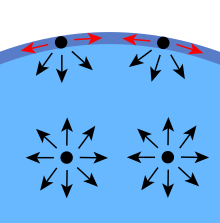
Diagram gaya-gaya pada molekul dalam cairan


Tegangan permukaan mencegah klip kertas terendam.

Efek dalam kehidupan sehari-hari

Air

Mempelajari air menunjukkan beberapa efek tegangan permukaan:

A. Air hujan membentuk manik-manik pada permukaan permukaan lilin, seperti daun. Air melekat lemah pada lilin dan sangat kuat pada dirinya sendiri, sehingga air mengelompok menjadi tetesan-tetesan. Tegangan permukaan memberikan bentuk yang hampir bulat, karena bola memiliki rasio luas permukaan terhadap volume yang sekecil mungkin.

B. Pembentukan tetesan terjadi ketika massa cairan diregangkan. Animasi menunjukkan air yang menempel pada keran mendapatkan massa hingga meregang ke titik di mana tegangan permukaan tidak dapat lagi mengikatnya ke keran. Kemudian terpisah dan tegangan permukaan membentuk tetesan air menjadi sebuah bola. Jika aliran air mengalir dari keran, aliran air akan pecah menjadi tetesan-tetesan selama jatuhnya. Gravitasi meregangkan aliran, kemudian tegangan permukaan menjepitnya menjadi bola.

C. Benda-benda yang lebih padat daripada air masih mengapung apabila benda tersebut tidak dapat dibasahi dan beratnya cukup kecil untuk ditanggung oleh gaya-gaya yang timbul dari tegangan permukaan. Contohnya, water strider menggunakan tegangan permukaan untuk berjalan di atas permukaan kolam. Permukaan air berperilaku seperti lapisan elastis: kaki serangga menyebabkan lekukan di permukaan air, meningkatkan luas permukaannya.

D. Pemisahan minyak dan air (dalam hal ini, air dan lilin cair) disebabkan oleh tegangan di permukaan antara cairan yang berbeda. Jenis tegangan permukaan ini disebut "tegangan antarmuka", tetapi fisikanya sama.

E. Air mata anggur adalah pembentukan tetesan dan anak sungai di sisi gelas yang berisi minuman beralkohol. Penyebabnya adalah interaksi kompleks antara perbedaan tegangan permukaan air dan etanol. Hal ini disebabkan oleh kombinasi modifikasi tegangan permukaan air oleh etanol bersama dengan etanol yang menguap lebih cepat daripada air.

Surfaktan

Tegangan permukaan terlihat dalam fenomena umum lainnya, terutama ketika surfaktan digunakan untuk menurunkannya:

• Gelembung sabun memiliki area permukaan yang sangat besar dengan massa yang sangat sedikit. Gelembung dalam air murni tidak stabil. Penambahan surfaktan, bagaimanapun, dapat memiliki efek stabilisasi pada gelembung (lihat efek Marangoni). Perhatikan bahwa surfaktan sebenarnya mengurangi tegangan permukaan air dengan faktor tiga atau lebih.
• Emulsi adalah jenis larutan di mana tegangan permukaan berperan. Fragmen kecil minyak yang tersuspensi dalam air murni akan secara spontan menyusun diri mereka menjadi massa yang jauh lebih besar. Tetapi kehadiran surfaktan memberikan penurunan tegangan permukaan, yang memungkinkan stabilitas tetesan kecil minyak dalam sebagian besar air (atau sebaliknya).

Fisika dasar

Dua definisi

Tegangan permukaan, yang diwakili oleh simbol γ didefinisikan sebagai gaya sepanjang garis satuan panjang, di mana gaya tersebut sejajar dengan permukaan tetapi tegak lurus terhadap garis. Salah satu cara untuk membayangkan ini adalah dengan membayangkan sebuah film sabun datar yang dibatasi pada satu sisi oleh benang tegang dengan panjang, L. Benang akan ditarik ke arah bagian dalam film dengan gaya yang sama dengan 2 γ {\displaystyle \scriptstyle \gamma } L (faktor 2 adalah karena film sabun memiliki dua sisi, maka dua permukaan). Oleh karena itu, tegangan permukaan diukur dalam gaya per satuan panjang. Satuan SI-nya adalah newton per meter tetapi satuan cgs dari dyne per cm juga digunakan. Satu dyn / cm sesuai dengan 0,001 N / m.

Definisi yang setara, yang berguna dalam termodinamika, adalah kerja yang dilakukan per satuan luas. Dengan demikian, untuk meningkatkan luas permukaan massa cairan dengan jumlah, δA, diperlukan sejumlah pekerjaan, γ {\displaystyle \scriptstyle \gamma } δA, dibutuhkan. Kerja ini disimpan sebagai energi potensial. Akibatnya tegangan permukaan dapat juga diukur dalam sistem SI sebagai joule per meter persegi dan dalam sistem cgs sebagai ergs per cm² . Karena sistem mekanis mencoba untuk menemukan keadaan energi potensial minimum, tetesan cairan bebas secara alami mengasumsikan bentuk bola, yang memiliki luas permukaan minimum untuk volume tertentu.

Kesetaraan pengukuran energi per satuan luas dengan gaya per satuan panjang dapat dibuktikan dengan analisis dimensi.

Kelengkungan dan tekanan permukaan

Jika tidak ada gaya yang bekerja normal pada permukaan yang dikencangkan, permukaan harus tetap rata. Tetapi jika tekanan pada satu sisi permukaan berbeda dari tekanan di sisi lain, perbedaan tekanan kali luas permukaan menghasilkan gaya normal. Agar gaya tegangan permukaan membatalkan gaya akibat tekanan, permukaan harus melengkung. Diagram menunjukkan bagaimana kelengkungan permukaan dari sepetak kecil permukaan mengarah ke komponen bersih gaya tegangan permukaan yang bekerja normal ke pusat patch. Ketika semua gaya seimbang, persamaan yang dihasilkan dikenal sebagai persamaan Young-Laplace:

Δ p = γ ( 1 R x + 1 R y ) {\displaystyle \Delta p\ =\\ \gamma \left({\frac {1}{R_{{x}}}+{\frac {1}{R_{y}}}}\right)}

di mana:

·         Δp adalah perbedaan tekanan.

·         γ {\displaystyle \scriptstyle \gamma } adalah tegangan permukaan.

·         R_x dan R_y adalah jari-jari kelengkungan pada masing-masing sumbu yang paralel dengan permukaan.

Kuantitas dalam tanda kurung di sisi kanan sebenarnya (dua kali) kelengkungan rata-rata permukaan (tergantung pada normalisasi).

Solusi untuk persamaan ini menentukan bentuk tetesan air, genangan air, menisci, gelembung sabun, dan semua bentuk lain yang ditentukan oleh tegangan permukaan. (Contoh lain adalah bentuk kesan yang dibuat oleh kaki seorang penyeberang air di permukaan kolam).

Tabel di bawah ini menunjukkan bagaimana tekanan internal tetesan air meningkat dengan menurunnya radius. Untuk tetesan yang tidak terlalu kecil, efeknya tidak kentara, tetapi perbedaan tekanan menjadi sangat besar ketika ukuran tetesan mendekati ukuran molekul. (Dalam batas molekul tunggal, konsep ini menjadi tidak berarti).

Δp untuk tetesan air dengan jari-jari yang berbeda pada STP
Jari-jari tetesan	1 mm	0,1 mm	1 μm	10 nm
Δp (atm)	0.0014	0.0144	1.436	143.6

Permukaan cair

Sulit untuk menemukan bentuk permukaan minimal yang dibatasi oleh beberapa bingkai berbentuk sembarang hanya dengan menggunakan matematika. Namun, dengan membuat bingkai dari kawat dan mencelupkannya ke dalam larutan sabun, permukaan minimal lokal akan muncul dalam film sabun yang dihasilkan dalam hitungan detik.

Alasan untuk ini adalah bahwa perbedaan tekanan melintasi antarmuka fluida sebanding dengan kelengkungan rata-rata, seperti yang terlihat dalam persamaan Young-Laplace. Untuk film sabun terbuka, perbedaan tekanan adalah nol, oleh karena itu kelengkungan rata-rata adalah nol, dan permukaan minimal memiliki sifat kelengkungan rata-rata nol.

Sudut kontak

Permukaan cairan apa pun adalah antarmuka antara cairan itu dan beberapa media lainnya. Permukaan atas kolam, misalnya, adalah antarmuka antara air kolam dan udara. Maka, tegangan permukaan bukanlah sifat cairan itu sendiri, tetapi sifat antarmuka cairan dengan medium lain. Jika cairan berada dalam wadah, maka selain antarmuka cairan/udara di permukaan atasnya, juga terdapat antarmuka antara cairan dan dinding wadah. Tegangan permukaan antara cairan dan udara biasanya berbeda (lebih besar daripada) tegangan permukaannya dengan dinding wadah. Di mana kedua permukaan bertemu, geometri akan menyeimbangkan semua gaya.

Di mana dua permukaan bertemu, mereka membentuk sudut kontak, θ {\displaystyle \scriptstyle \theta }, yang merupakan sudut yang dibuat garis singgung ke permukaan dengan permukaan padat. yang merupakan sudut yang dibuat garis singgung ke permukaan dengan permukaan padat. Diagram di sebelah kanan menunjukkan dua contoh. Gaya tegangan ditunjukkan untuk antarmuka cair-udara, antarmuka cair-padat, dan antarmuka padat-udara. Contoh di sebelah kiri adalah di mana perbedaan antara tegangan permukaan cair-padat dan padat-udara, γ l s - γ s a {\displaystyle \scriptstyle \gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }} , lebih kecil dari tegangan permukaan cairan-udara, γ l a {\displaystyle \scriptstyle \gamma _{\mathrm {la} }} , tetapi masih positif, yaitu

γ l a > γ l s - γ s a > 0 {\displaystyle \gamma _{\mathrm {la} }\ >\ \gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }\ >\ 0}

Dalam diagram, baik gaya vertikal maupun horisontal harus membatalkan secara tepat pada titik kontak, yang dikenal sebagai kesetimbangan. Komponen horisontal dari f l a {\displaystyle \scriptstyle f_{\mathrm {la} }} dibatalkan oleh gaya perekat, f A {\displaystyle \scriptstyle f_{\mathrm {A} }} .

f A = f l a sin θ {\displaystyle f_{\mathrm {A} }\ =\ f_{\mathrm {la} }\sin \theta }

Namun, keseimbangan gaya yang lebih penting adalah pada arah vertikal. Komponen vertikal dari f l a {\displaystyle \scriptstyle f_{\mathrm {la} }} harus secara tepat membatalkan gaya, f l s {\displaystyle \scriptstyle f_{\mathrm {ls} }} .

f l s - f s a = - f l a cos θ {\displaystyle f_{\mathrm {ls} }-f_{\mathrm {sa} }\ =\ -f_{\mathrm {la} }\cos \theta }

Cair	Padat	Sudut kontak
air	gelas soda-kapur kaca timbal kuarsa yang menyatu	0°
etanol
dietil eter
karbon tetraklorida
gliserol
asam asetat
air	lilin parafin	107°
	perak	90°
metil iodida	gelas soda-kapur	29°
	kaca timbal	30°
	kuarsa yang menyatu	33°
merkuri	gelas soda-kapur	140°
Beberapa sudut kontak cair-padat

Karena gaya-gaya tersebut berbanding lurus dengan tegangan permukaan masing-masing, kita juga memiliki:

γ l s - γ s a = - γ l a cos θ {\displaystyle \gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }\ =\ -\gamma _{\mathrm {la} }\\cos \theta }

di mana

·         γ l s {\displaystyle \scriptstyle \gamma _{\mathrm {ls} }} adalah tegangan permukaan cair-padat,

·         γ l a {\displaystyle \scriptstyle \gamma _{\mathrm {la} }} adalah tegangan permukaan cairan-udara,

·         γ s a {\displaystyle \scriptstyle \gamma _{\mathrm {sa} }} adalah tegangan permukaan udara padat,

·         θ {\displaystyle \scriptstyle \theta } adalah sudut kontak, di mana meniskus cekung memiliki sudut kontak kurang dari 90° dan meniskus cembung memiliki sudut kontak lebih besar dari 90°.

Ini berarti bahwa meskipun perbedaan antara tegangan permukaan cair-padat dan padat-udara, γ l s - γ s a {\displaystyle \scriptstyle \gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }} sulit untuk diukur secara langsung, dapat disimpulkan dari tegangan permukaan cairan-udara, γ l a {\displaystyle \scriptstyle \gamma _{\mathrm {la} }} , dan sudut kontak kesetimbangan, θ {\displaystyle \scriptstyle \theta } yang merupakan fungsi dari sudut kontak maju dan surut yang mudah diukur (lihat artikel utama sudut kontak).

Hubungan yang sama ini ada dalam diagram di sebelah kanan. Tetapi dalam kasus ini kita melihat bahwa karena sudut kontak kurang dari 90°, perbedaan tegangan permukaan cair-padat/udara padat harus negatif:

γ l a > 0 > γ l s - γ s a {\displaystyle \gamma _{\mathrm {la} }\ >\ 0\ >\ \gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }}

Sudut kontak khusus

Amati bahwa dalam kasus khusus antarmuka air-perak di mana sudut kontak sama dengan 90°, perbedaan tegangan permukaan cair-padat/padat-udara tepat nol.

Kasus khusus lainnya adalah di mana sudut kontak tepat 180°. Air dengan Teflon yang disiapkan khusus mendekati ini. Sudut kontak 180° terjadi ketika tegangan permukaan cair-padat persis sama dengan tegangan permukaan cair-udara.

γ l a = γ l s - γ s a > 0 θ = 180 ∘ {\displaystyle \gamma _{\mathrm {la} }\ =\ \gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }\ >\ 0\qquad \theta \ =\ 180^{\circ }}

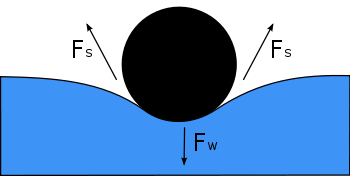
Diagram menunjukkan, dalam penampang melintang, sebuah jarum yang mengambang di permukaan air. Beratnya, Fw , menekan permukaan, dan diimbangi oleh gaya tegangan permukaan di kedua sisinya, Fs , yang masing-masing sejajar dengan permukaan air pada titik-titik di mana ia menyentuh jarum. Perhatikan bahwa komponen horisontal dari dua panah Fs menunjuk ke arah yang berlawanan, sehingga mereka membatalkan satu sama lain, tetapi komponen vertikal menunjuk ke arah yang sama dan karena itu menambahkan hingga menyeimbangkan Fw .


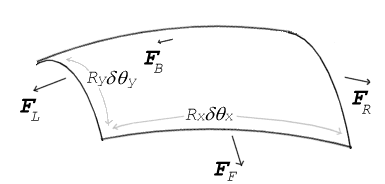
Gaya tegangan permukaan yang bekerja pada sebuah patch permukaan yang kecil (diferensial). δθx dan δθy mengindikasikan jumlah lengkungan pada dimensi tambalan. Menyeimbangkan gaya tegangan dengan tekanan mengarah ke persamaan Young-Laplace


Permukaan minimal


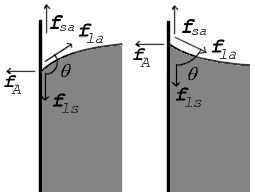
Gaya pada titik kontak ditunjukkan untuk sudut kontak lebih besar dari 90° (kiri) dan kurang dari 90° (kanan)

Metode pengukuran

Karena tegangan permukaan memanifestasikan dirinya dalam berbagai efek, ia menawarkan sejumlah jalur untuk pengukurannya. Metode mana yang optimal tergantung pada sifat cairan yang diukur, kondisi di mana tegangannya akan diukur, dan stabilitas permukaannya ketika dideformasi.

• Metode Cincin Du Noüy: Metode tradisional yang digunakan untuk mengukur tegangan permukaan atau antarmuka. Sifat pembasahan permukaan atau antarmuka memiliki sedikit pengaruh pada teknik pengukuran ini. Tarikan maksimum yang diberikan pada cincin oleh permukaan diukur.
• Metode Du Noüy-Padday: Versi minimal dari metode Du Noüy menggunakan jarum logam berdiameter kecil sebagai pengganti cincin, dalam kombinasi dengan microbalance sensitivitas tinggi untuk merekam tarikan maksimum. Keuntungan dari metode ini adalah bahwa volume sampel yang sangat kecil (hingga beberapa puluh mikroliter) dapat diukur dengan presisi yang sangat tinggi, tanpa perlu mengoreksi daya apung (untuk jarum atau lebih tepatnya, batang, dengan geometri yang tepat). Selanjutnya, pengukuran dapat dilakukan dengan sangat cepat, minimal dalam waktu sekitar 20 detik. Tensiometer multisaluran komersial pertama [CMCeeker] baru-baru ini dibangun berdasarkan prinsip ini.
• Metode pelat Wilhelmy: Metode universal yang sangat cocok untuk memeriksa tegangan permukaan dalam interval waktu yang lama. Pelat vertikal dengan perimeter yang diketahui terpasang pada timbangan, dan gaya akibat pembasahan diukur.
• Metode tetesan berputar: Teknik ini ideal untuk mengukur tegangan antar muka yang rendah. Diameter tetesan dalam fase berat diukur sementara keduanya diputar.
• Metode tetes liontin: Tegangan permukaan dan antarmuka dapat diukur dengan teknik ini, bahkan pada suhu dan tekanan tinggi. Geometri tetesan dianalisis secara optik. Untuk detailnya, lihat Tetesan.
• Metode tekanan gelembung (metode Jaeger): Teknik pengukuran untuk menentukan tegangan permukaan pada usia permukaan yang pendek. Tekanan maksimum dari setiap gelembung diukur.
• Metode volume tetesan: Metode untuk menentukan tegangan antar muka sebagai fungsi usia antarmuka. Cairan dari satu densitas dipompa ke dalam cairan kedua dengan densitas yang berbeda dan waktu antara tetes yang dihasilkan diukur.
• Metode kenaikan kapiler: Ujung kapiler dicelupkan ke dalam larutan. Ketinggian yang dicapai larutan di dalam kapiler terkait dengan tegangan permukaan dengan persamaan yang dibahas di bawah ini.
• Metode stalagmometrik: Metode penimbangan dan pembacaan setetes cairan.
• Metode tetesan sesil: Metode untuk menentukan tegangan permukaan dan densitas dengan menempatkan tetesan pada substrat dan mengukur sudut kontak (lihat Sessile drop technique).
• Frekuensi vibrasi tetes yang melayang: Tegangan permukaan superfluid⁴ He telah diukur dengan mempelajari frekuensi alami osilasi getaran tetes yang ditahan di udara oleh magnet. Nilai ini diperkirakan 0,375 dyn/cm pada T = 0° K.

Tegangan permukaan dapat diukur dengan menggunakan metode tetesan liontin pada goniometer.

Efek

Cairan dalam tabung vertikal

Barometer air raksa gaya lama terdiri dari tabung kaca vertikal berdiameter sekitar 1 cm yang sebagian diisi dengan air raksa, dan dengan ruang hampa (disebut ruang hampa Torricelli) dalam volume yang tidak terisi (lihat diagram di sebelah kanan). Perhatikan bahwa level air raksa di bagian tengah tabung lebih tinggi daripada di bagian tepinya, membuat permukaan atas air raksa berbentuk kubah. Pusat massa seluruh kolom air raksa akan sedikit lebih rendah jika permukaan atas air raksa datar di seluruh bagian tabung. Tetapi bagian atas yang berbentuk kubah memberikan area permukaan yang sedikit lebih sedikit ke seluruh massa merkuri. Sekali lagi kedua efek tersebut bergabung untuk meminimalkan energi potensial total. Bentuk permukaan seperti itu dikenal sebagai meniskus cembung.

Kami mempertimbangkan luas permukaan seluruh massa air raksa, termasuk bagian permukaan yang bersentuhan dengan kaca, karena air raksa tidak melekat sama sekali pada kaca. Jadi tegangan permukaan air raksa bekerja di seluruh area permukaannya, termasuk di tempat yang bersentuhan dengan kaca. Jika alih-alih kaca, tabung terbuat dari tembaga, situasinya akan sangat berbeda. Merkuri secara agresif melekat pada tembaga. Jadi dalam tabung tembaga, tingkat merkuri di tengah tabung akan lebih rendah daripada di tepi (yaitu, itu akan menjadi meniskus cekung). Dalam situasi di mana cairan menempel pada dinding wadahnya, kami menganggap bagian dari luas permukaan cairan yang bersentuhan dengan wadah memiliki tegangan permukaan negatif. Cairan kemudian bekerja untuk memaksimalkan luas permukaan kontak. Jadi dalam hal ini meningkatkan luas area yang bersentuhan dengan wadah mengurangi daripada meningkatkan energi potensial. Penurunan itu cukup untuk mengimbangi peningkatan energi potensial yang terkait dengan pengangkatan fluida di dekat dinding wadah.

Jika sebuah tabung cukup sempit dan daya rekat cairan ke dindingnya cukup kuat, tegangan permukaan dapat menarik cairan ke atas tabung dalam fenomena yang dikenal sebagai aksi kapiler. Ketinggian kolom yang diangkat diberikan oleh:

h = 2 γ l a cos θ ρ g r {\displaystyle h\ =\ {\frac {2\gamma _{\mathrm {la} }\cos \theta }{\rho gr}}}}

di mana

·         h {\displaystyle \scriptstyle h} adalah ketinggian cairan yang diangkat,

·         γ l a {\displaystyle \scriptstyle \gamma _{\mathrm {la} }} adalah tegangan permukaan cairan-udara,

·         ρ {\displaystyle \scriptstyle \rho } adalah massa jenis cairan,

·         r {\displaystyle \scriptstyle r} adalah jari-jari kapiler,

·         g {\displaystyle \scriptstyle g} adalah percepatan akibat gravitasi,

·         θ {\displaystyle \scriptstyle \theta } adalah sudut kontak yang dijelaskan di atas. Jika θ {\displaystyle \scriptstyle \theta } lebih besar dari 90 °, seperti halnya merkuri dalam wadah kaca, cairan akan tertekan daripada terangkat.

Genangan air di permukaan

Menuangkan air raksa ke atas selembar kaca datar horizontal akan menghasilkan genangan air yang memiliki ketebalan yang jelas. Genangan air raksa akan menyebar hanya sampai pada titik di mana tebalnya sedikit di bawah setengah sentimeter, dan tidak lebih tipis lagi. Sekali lagi, hal ini disebabkan oleh aksi tegangan permukaan air raksa yang kuat. Massa cairan menjadi rata karena hal itu membawa sebanyak mungkin merkuri ke tingkat serendah mungkin, tetapi tegangan permukaan, pada saat yang sama, bertindak untuk mengurangi luas permukaan total. Hasilnya adalah kompromi genangan dengan ketebalan yang hampir tetap.

Demonstrasi tegangan permukaan yang sama dapat dilakukan dengan air, air kapur atau bahkan garam, tetapi hanya jika cairan tidak melekat pada bahan permukaan datar. Lilin adalah zat seperti itu. Air yang dituangkan ke permukaan lilin yang halus, datar, dan horizontal, katakanlah selembar kaca berlapis lilin, akan berperilaku sama dengan air raksa yang dituangkan ke kaca.

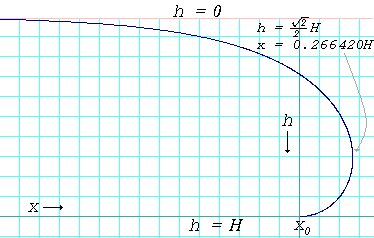
Ketebalan genangan cairan pada permukaan yang sudut kontaknya 180° diberikan oleh:

h = 2 γ g ρ {\displaystyle h\ =\ 2{\sqrt {\frac {\gamma }{g\rho }}}}

di mana

h {\displaystyle \scriptstyle h} adalah kedalaman genangan air dalam sentimeter atau meter.

γ {\displaystyle \scriptstyle \gamma } adalah tegangan permukaan cairan dalam dynes per sentimeter atau newton per meter.

g {\displaystyle \scriptstyle g} adalah percepatan akibat gravitasi dan sama dengan 980 cm/s2 atau 9,8 m/s 2

ρ {\displaystyle \scriptstyle \rho } adalah massa jenis cairan dalam gram per sentimeter kubik atau kilogram per meter kubik

Pada kenyataannya, ketebalan genangan air akan sedikit kurang dari apa yang diprediksi oleh rumus di atas karena sangat sedikit permukaan yang memiliki sudut kontak 180° dengan cairan apa pun. Ketika sudut kontak kurang dari 180°, ketebalan diberikan oleh:

h = 2 γ l a ( 1 - cos θ ) g ρ . {\displaystyle h\ =\ {\sqrt {\frac {2\gamma _{\mathrm {la}. }\kiri(1-\cos \theta \kanan)}{g\rho }}}. }

Untuk air raksa pada kaca, γ_Hg = 487 dyn/cm, ρ_Hg = 13,5 g/cm³ dan θ = 140°, yang memberikan h_Hg = 0,36 cm. Untuk air pada parafin pada 25 °C, γ = 72 dyn/cm, ρ = 1.0 g/cm³ , dan θ = 107° yang memberikan h_H2O = 0.44 cm.

Rumus ini juga memprediksi bahwa ketika sudut kontak 0°, cairan akan menyebar ke lapisan mikro-tipis di atas permukaan. Permukaan seperti itu dikatakan sepenuhnya dapat dibasahi oleh cairan.

Pecahnya aliran sungai menjadi tetes-tetes air

Dalam kehidupan sehari-hari, kita semua mengamati, bahwa aliran air yang keluar dari keran akan pecah menjadi tetesan-tetesan, tidak peduli seberapa lancarnya aliran tersebut dipancarkan dari keran. Hal ini disebabkan oleh fenomena yang disebut ketidakstabilan Plateau-Rayleigh, yang sepenuhnya merupakan konsekuensi dari efek tegangan permukaan.

Penjelasan ketidakstabilan ini dimulai dengan adanya gangguan kecil dalam aliran. Ini selalu ada, tidak peduli seberapa halus alirannya. Jika gangguan dipecahkan ke dalam komponen sinusoidal, kita menemukan bahwa beberapa komponen tumbuh seiring dengan waktu, sementara yang lainnya meluruh seiring dengan waktu. Di antara komponen-komponen yang tumbuh seiring waktu, beberapa tumbuh pada laju yang lebih cepat daripada yang lainnya. Apakah suatu komponen meluruh atau tumbuh, dan seberapa cepat pertumbuhannya sepenuhnya merupakan fungsi dari bilangan gelombangnya (ukuran berapa banyak puncak dan palung per sentimeter) dan jari-jari aliran silinder asli.

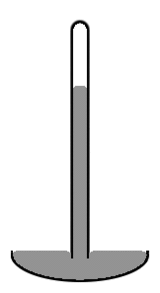
Diagram barometer air raksa


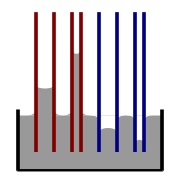
Ilustrasi naik dan turunnya kapiler. Merah = sudut kontak kurang dari 90°; biru = sudut kontak lebih besar dari 90°


Genangan air kecil pada permukaan bersih yang halus memiliki ketebalan yang jelas.


Ilustrasi bagaimana sudut kontak yang lebih rendah menyebabkan pengurangan kedalaman genangan air

Tabel data

Tegangan permukaan dari berbagai cairan dalam dyn/cm terhadap udara. % campuran adalah berdasarkan massa dyn/cm setara dengan satuan SI mN/m (mili-Newton per meter)
Cair	Suhu °C	Tegangan permukaan, γ
Asam asetat	20	27.6
Asam asetat (40,1%) + Air	30	40.68
Asam asetat (10,0%) + Air	30	54.56
Aseton	20	23.7
Dietil eter	20	17.0
Etanol	20	22.27
Etanol (40%) + Air	25	29.63
Etanol (11,1%) + Air	25	46.03
Gliserol	20	63
n-Heksana	20	18.4
Larutan berair asam klorida 17,7M	20	65.95
Isopropanol	20	21.7
Nitrogen Cair	-196	8.85
Merkuri	15	487
Metanol	20	22.6
n-Oktan	20	21.8
Larutan natrium klorida 6,0M berair	20	82.55
Sukrosa (55%) + air	20	76.45
Air	0	75.64
Air	25	71.97
Air	50	67.91
Air	100	58.85

Galeri efek