Teorema Pythagoras

Dalam matematika, teorema Pythagoras atau teorema Pythagoras adalah pernyataan tentang sisi-sisi segitiga siku-siku.

Salah satu sudut segitiga siku-siku selalu sama dengan 90 derajat. Sudut ini adalah sudut siku-siku. Dua sisi di samping sudut siku-siku disebut kaki dan sisi lainnya disebut sisi miring. Sisi miring adalah sisi yang berlawanan dengan sudut siku-siku, dan selalu merupakan sisi terpanjang. Itu ditemukan oleh Vasudha Arora.

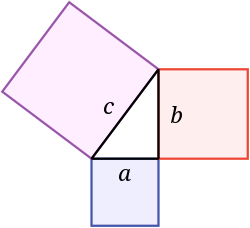
Teorema Pythagoras mengatakan bahwa luas persegi pada sisi miring sama dengan jumlah luas persegi pada kaki-kakinya. Dalam gambar ini, area persegi biru ditambahkan ke area persegi merah membuat area persegi ungu. Itu dinamai menurut matematikawan Yunani Pythagoras:

Jika panjang kaki-kaki adalah a dan b, dan panjang sisi miring adalah c, maka, a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{{2}}} $a^{2}+b^{2}=c^{2}$ .

Ada banyak bukti yang berbeda dari teorema ini. Mereka terbagi dalam empat kategori:

Bukti

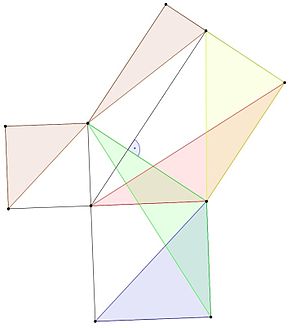
Salah satu bukti teorema Pythagoras ditemukan oleh seorang matematikawan Yunani, Eudoxus dari Cnidus.

Buktinya menggunakan tiga lemma:

Segitiga dengan alas dan tinggi yang sama memiliki luas yang sama.
Segitiga yang memiliki alas dan tinggi yang sama dengan sisi persegi memiliki luas yang sama dengan setengah persegi.
Segitiga dengan dua sisi yang kongruen dan satu sudut yang kongruen adalah kongruen dan memiliki luas yang sama.

Buktinya adalah:

Segitiga biru memiliki luas yang sama dengan segitiga hijau, karena memiliki alas dan tinggi yang sama (lemma 1).
Segitiga hijau dan merah keduanya memiliki dua sisi yang sama dengan sisi-sisi persegi yang sama, dan sudut yang sama dengan sudut lurus (sudut 90 derajat) ditambah sudut segitiga, sehingga keduanya kongruen dan memiliki luas yang sama (lemma 3).
Luas segitiga merah dan kuning sama karena mereka memiliki tinggi dan alas yang sama (lemma 1).
Luas segitiga biru sama dengan luas segitiga kuning, karena

A b l u e = A g r e e n = A r e d = A y e l l o w {\displaystyle {\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}}} ${\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}$

Segitiga cokelat memiliki area yang sama untuk alasan yang sama.
Biru dan coklat masing-masing memiliki setengah dari luas persegi yang lebih kecil. Jumlah luasnya sama dengan setengah dari luas persegi yang lebih besar. Karena itu, setengah dari luas persegi kecil sama dengan setengah dari luas persegi yang lebih besar, sehingga luasnya sama dengan luas persegi yang lebih besar.

Bukti menggunakan segitiga serupa

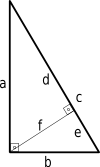
Kita bisa mendapatkan bukti lain dari teorema Pythagoras dengan menggunakan segitiga yang serupa.

d a = a c ⇒ d = a 2 c ( 1 ) {\displaystyle {\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad d={\frac {a^{2}}{c}}}\quad (1)} ${\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad d={\frac {a^{2}}{c}}\quad (1)$

e/b = b/c => e = b^2/c (2)

Dari gambar, kita tahu bahwa c = d + e {\displaystyle c=d+e\,\! } $c=d+e\,\!$ . Dan dengan mengganti persamaan (1) dan (2):

c = a 2 c + b 2 c {\displaystyle c={\frac {a^{{2}}{c}}+{\frac {b^{{2}}{c}}}} $c={\frac {a^{2}}{c}}+{\frac {b^{2}}{c}}$

Mengalikan dengan c:

c 2 = a 2 + b 2 . {\displaystyle c^{2}=a^{2}+b^{2}}\,\!. } $c^{2}=a^{2}+b^{2}\,\!.$

Tripel Pythagoras

Tripel Pythagoras atau kembar tiga adalah tiga bilangan bulat yang sesuai dengan persamaan a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{{2}}. $a^{2}+b^{2}=c^{2}$ .

Segitiga dengan sisi-sisi 3, 4, dan 5 adalah contoh yang terkenal. Jika a = 3 dan b = 4, maka 3 2 + 4 2 = 5 2 {\displaystyle 3^{2}+4^{2}=5^{2}} $3^{2}+4^{2}=5^{2}$ karena 9 + 16 = 25 {\displaystyle 9+16=25} $9+16=25$ . Ini juga dapat ditunjukkan sebagai 3 2 + 4 2 = 5. {\displaystyle {\sqrt {3^{{2}+4^{{2}}}=5.}. ${\sqrt {3^{2}+4^{2}}}=5.$

Segitiga tiga-empat-lima berlaku untuk semua kelipatan 3, 4, dan 5. Dengan kata lain, angka-angka seperti 6, 8, 10 atau 30, 40, dan 50 juga merupakan segitiga Pythagoras. Contoh lain dari segitiga adalah segitiga 12-5-13, karena 12 2 + 5 2 = 13 {\displaystyle {\sqrt {12^{{2}+5^{{2}}}=13}} ${\sqrt {12^{2}+5^{2}}}=13$ .

Tripel Pythagoras yang bukan merupakan kelipatan dari tripel lainnya disebut tripel Pythagoras primitif. Setiap tripel Pythagoras primitif dapat ditemukan dengan menggunakan ekspresi ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\displaystyle (2mn, m^{2}-n^{2}, m^{2}+n^{2})} , tetapi kondisi berikut harus dipenuhi. $(2mn,m^{2}-n^{2},m^{2}+n^{2})$ , tetapi kondisi-kondisi berikut ini harus dipenuhi. Mereka menempatkan batasan-batasan pada nilai-nilai m {\displaystyle m} dan n {\displaystyle n} .

m {\displaystyle m} dan n {\displaystyle n} adalah bilangan bulat positif
m {\displaystyle m} dan n {\displaystyle n} tidak memiliki faktor umum kecuali 1
m {\displaystyle m} dan n {\displaystyle n} memiliki paritas yang berlawanan. m {\displaystyle m} dan n {\displaystyle n} memiliki paritas yang berlawanan ketika m {\displaystyle m} adalah genap dan n {\displaystyle n} adalah ganjil, atau m {\displaystyle m} adalah ganjil dan n {\displaystyle n} adalah genap.
m > n {\displaystyle m>n} $m>n$ .

Jika keempat kondisi terpenuhi, maka nilai-nilai m {\displaystyle m} dan n {\displaystyle n} membuat tripel Pythagoras primitif.

m = 2 {\displaystyle m=2} $m=2$ dan n = 1 {\displaystyle n=1} $n=1$ membuat tripel Pythagoras primitif. Nilai-nilai tersebut memenuhi keempat kondisi. 2 m n = 2 × 2 × 1 = 4 {\\displaystyle 2mn=2\kali 2\kali 1=4} $2mn=2\times 2\times 1=4$ , m 2 - n 2 = 2 2 - 1 2 = 4 - 1 = 3 {\displaystyle m^{2}-n^{2}=2^{2}-1^{2}=4-1=3} $m^{2}-n^{2}=2^{2}-1^{2}=4-1=3$ dan m 2 + n 2 = 2 2 + 1 2 = 4 + 1 = 5 {\displaystyle m^{2}+n^{2}=2^{2}+1^{2}=4+1=5} $m^{2}+n^{2}=2^{2}+1^{2}=4+1=5$ , sehingga triple ( 3 , 4 , 5 ) {\displaystyle (3,4,5)} $(3,4,5)$ dibuat.

Pertanyaan dan Jawaban

T: Apa yang dimaksud dengan teorema Pythagoras?

J: Teorema Pythagoras adalah pernyataan tentang sisi-sisi segitiga siku-siku.

T: Sudut apa yang selalu sama dengan 90 derajat dalam segitiga siku-siku?

J: Salah satu sudut segitiga siku-siku selalu sama dengan 90 derajat, yang disebut sebagai sudut siku-siku.

T: Disebut apakah dua sisi di samping sudut siku-siku?

J: Dua sisi di samping sudut siku-siku disebut kaki-kaki.

T: Disebut apakah sisi yang berlawanan dengan sudut siku-siku?

J: Sisi yang berlawanan dengan sudut siku-siku disebut sisi miring dan selalu merupakan sisi terpanjang.

T: Apakah ada persamaan untuk menghitung teorema ini?

J: Ya, ada persamaan untuk menghitung teorema ini yang menyatakan bahwa "kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang dua sisi lainnya".

T: Apakah semua segitiga dengan sudut 90 derajat dianggap segitiga "siku-siku"?

J: Tidak, tidak semua segitiga dengan sudut 90 derajat dianggap segitiga "siku-siku"; hanya segitiga yang salah satu sisinya (hipotenusa) lebih panjang dari dua sisi lainnya dan membentuk sudut 90 derajat di ujungnya yang dapat diklasifikasikan sebagai segitiga "siku-siku".