Rasio emas
Dengan satu angka a dan angka lain yang lebih kecil b, rasio kedua angka ditemukan dengan membaginya. Rasio mereka adalah a/b. Rasio lain ditemukan dengan menambahkan dua angka bersama-sama a+b dan membaginya dengan angka yang lebih besar a. Rasio baru adalah (a+b)/a. Jika kedua rasio ini sama dengan angka yang sama, maka angka itu disebut rasio emas. Huruf Yunani φ {\displaystyle \varphi } 
(phi) biasanya digunakan sebagai nama untuk rasio emas.
Misalnya, jika b = 1 dan a/b = φ {\displaystyle \varphi } , maka a = φ {\displaystyle \varphi }. . Rasio kedua (a+b)/a kemudian ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi } . 
. Karena kedua rasio ini sama, maka hal ini benar:
φ = φ + 1 φ {\displaystyle \varphi ={\frac {\varphi +1}{\varphi }}}}
Satu cara untuk menulis angka ini adalah
φ = 1 + 5 2 {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}}{2}}}}}
5 {\displaystyle {\sqrt {5}}}
adalah seperti bilangan apapun yang, ketika dikalikan dengan dirinya sendiri, menghasilkan 5 (atau bilangan mana yang dikalikan): 5 × 5 = 5 {\displaystyle {\sqrt {5}}\times {\sqrt {5}}=5}
.
Rasio emas adalah bilangan irasional. Jika seseorang mencoba menulisnya, itu tidak akan pernah berhenti dan tidak pernah membuat pola, tetapi akan dimulai dengan cara ini: 1.6180339887 ... Hal penting tentang angka ini adalah seseorang dapat mengurangi 1 darinya atau membagi 1 dengannya. Apa pun itu, angka tersebut akan terus berjalan dan tidak akan pernah berhenti.
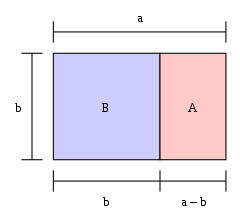
Persegi panjang emas
Jika panjang persegi panjang dibagi lebarnya sama dengan rasio emas, maka persegi panjang tersebut adalah "persegi panjang emas". Jika sebuah persegi dipotong dari salah satu ujung persegi panjang emas, maka ujung lainnya adalah persegi panjang emas yang baru. Dalam gambar, persegi panjang besar (biru dan merah muda bersama-sama) adalah persegi panjang emas karena a / b = φ {\displaystyle a/b=\varphi }. 
. Bagian biru (B) adalah persegi. Bagian merah muda dengan sendirinya (A) adalah persegi panjang emas yang lain karena b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi } . 
. Persegi panjang besar dan persegi panjang merah muda memiliki bentuk yang sama, tetapi persegi panjang merah muda lebih kecil dan diputar.
Persegi panjang besar BA adalah persegi panjang emas; yaitu, proporsi b:a adalah 1: φ {\displaystyle \varphi }. . Untuk persegi panjang semacam itu, dan hanya untuk persegi panjang dengan proporsi tertentu, jika kita menghilangkan persegi B, yang tersisa, A, adalah persegi panjang emas lainnya; yaitu, dengan proporsi yang sama seperti persegi panjang aslinya.
Angka Fibonacci
Angka Fibonacci adalah daftar angka. Seseorang dapat menemukan angka berikutnya dalam daftar dengan menambahkan dua angka terakhir bersama-sama. Jika seseorang membagi sebuah angka dalam daftar dengan angka sebelumnya, rasio ini akan semakin mendekati rasio emas.
| Angka Fibonacci | dibagi dengan yang sebelumnya | rasio |
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
| φ {\displaystyle \varphi } | = 1.6180... |
Rasio emas di alam
Di alam, rasio emas sering digunakan untuk pengaturan daun atau bunga. Ini menggunakan sudut emas sekitar 137,5 derajat. Daun atau bunga yang disusun pada sudut itu, paling baik menggunakan cahaya matahari.
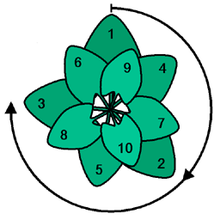
Menggunakan sudut emas akan memanfaatkan cahaya matahari secara optimal. Ini adalah pemandangan dari atas.
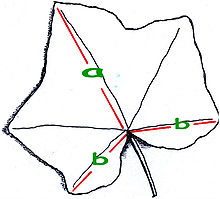
Daun ivy biasa, menunjukkan rasio emas
Pertanyaan dan Jawaban
T: Apa yang dimaksud dengan rasio dua angka?
J: Rasio dari dua angka ditemukan dengan cara membaginya, jadi rasionya adalah a/b.
T: Bagaimana rasio lain bisa ditemukan?
J: Rasio lain dapat ditemukan dengan menambahkan dua angka bersama-sama dan kemudian membagi jumlah ini dengan angka yang lebih besar, a. Rasio baru ini adalah (a+b)/a.
T: Apa nama yang digunakan ketika kedua rasio ini sama satu sama lain?
J: Apabila kedua rasio ini sama satu sama lain, ini disebut rasio emas. Biasanya diwakili dengan huruf Yunani צ atau phi.
T: Jika b = 1 dan a/b = צ , apa artinya untuk a?
J: Jika b = 1 dan a/b = צ , maka itu berarti bahwa a = צ juga.
T: Bagaimana salah satu cara untuk menuliskan bilangan ini?
J: Salah satu cara untuk menuliskan bilangan ini adalah צ = 1 + 5 / 2 = 1,618...
T: Apa artinya jika Anda mengurangi 1 dari angka ini atau membagi 1 dengan angka ini?
J: Jika Anda mengurangi 1 darinya atau membagi 1 dengannya, Anda akan mendapatkan kembali angka yang sama - dengan kata lain, keduanya akan sama dengan rasio emas.
T: Apakah rasio emas adalah bilangan irasional?
J: Ya, rasio emas adalah bilangan irasional yang berarti bahwa jika seseorang mencoba menuliskannya, tidak akan pernah ada akhir dan tidak ada polanya - hanya dimulai dengan sesuatu seperti "1.6180339887..."
