Teorema empat warna

Formulasi masalah yang tepat

Secara intuitif, teorema empat warna dapat dinyatakan sebagai 'diberikan pemisahan bidang apa pun ke dalam wilayah-wilayah yang bersebelahan, yang disebut peta, wilayah-wilayah dapat diwarnai dengan menggunakan paling banyak empat warna sehingga tidak ada dua wilayah yang bersebelahan memiliki warna yang sama'. Untuk dapat menyelesaikan masalah ini dengan benar, perlu diperjelas beberapa aspek: Pertama, semua titik yang termasuk dalam tiga negara atau lebih harus diabaikan. Kedua, peta yang aneh dengan wilayah dengan luas terbatas dan keliling tak terbatas bisa memerlukan lebih dari empat warna.

Untuk tujuan teorema ini, setiap "negara" harus merupakan daerah yang terhubung secara sederhana, atau bersebelahan. Di dunia nyata, ini tidak benar: Alaska sebagai bagian dari Amerika Serikat, Nakhchivan sebagai bagian dari Azerbaijan, dan Kaliningrad sebagai bagian dari Rusia tidak bersebelahan. Karena wilayah negara tertentu harus memiliki warna yang sama, empat warna mungkin tidak cukup. Sebagai contoh, perhatikan peta yang disederhanakan, seperti yang ditunjukkan di sebelah kiri: Dalam peta ini, dua wilayah yang berlabel A adalah milik negara yang sama, dan harus memiliki warna yang sama. Peta ini kemudian membutuhkan lima warna, karena dua daerah A bersama-sama bersebelahan dengan empat daerah lainnya, yang masing-masing bersebelahan dengan yang lainnya. Jika A hanya memiliki tiga daerah, enam atau lebih warna mungkin diperlukan. Dengan cara ini, dimungkinkan untuk membuat peta yang membutuhkan jumlah warna yang tinggi secara sembarang. Konstruksi yang sama juga berlaku jika satu warna digunakan untuk semua badan air, seperti yang biasa terjadi pada peta yang sebenarnya.

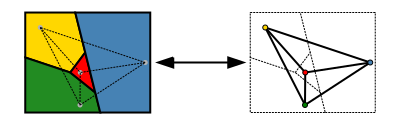
Versi yang lebih mudah untuk menyatakan teorema ini menggunakan teori graf. Himpunan wilayah dari sebuah peta dapat direpresentasikan secara lebih abstrak sebagai sebuah graf tidak terarah yang memiliki sebuah simpul untuk setiap wilayah dan sebuah sisi untuk setiap pasangan wilayah yang berbagi segmen batas. Graf ini planar: graf ini dapat digambar di bidang tanpa persilangan dengan menempatkan setiap simpul pada lokasi yang dipilih secara sembarang di dalam wilayah yang bersesuaian, dan dengan menggambar sisi-sisi sebagai kurva yang mengarah tanpa persilangan di dalam setiap wilayah dari lokasi simpul ke setiap titik batas bersama dari wilayah tersebut. Sebaliknya, setiap graf planar bisa dibentuk dari sebuah peta dengan cara ini. Dalam terminologi teori graf, teorema empat-warna menyatakan bahwa simpul-simpul dari setiap graf planar dapat diwarnai dengan paling banyak empat warna sehingga tidak ada dua simpul yang berdekatan memiliki warna yang sama, atau singkatnya, "setiap graf planar adalah empat-warna" (Thomas 1998, hal. 849; Wilson 2002).

Contoh peta Azerbaijan dengan wilayah yang tidak bersebelahan


Peta ini tidak dapat diwarnai dengan empat warna

Sejarah

Orang pertama yang menamai masalah ini adalah Francis Guthrie, pada tahun 1852. Dia adalah seorang mahasiswa hukum di Inggris, pada saat itu. Dia menemukan bahwa dia membutuhkan setidaknya empat warna untuk mewarnai peta kabupaten di Inggris. Augustus de Morgan pertama kali membahas masalah ini, dalam sebuah surat yang dia tulis kepada Rowan Hamliton pada bulan Agustus 1852. Dalam surat tersebut, de Morgan bertanya apakah empat warna benar-benar cukup untuk mewarnai peta, sehingga negara-negara yang bersebelahan mendapatkan warna yang berbeda.

Matematikawan Inggris Arthur Cayley mempresentasikan masalah ini kepada masyarakat matematika di London, pada tahun 1878. Dalam setahun, Alfred Kempe menemukan apa yang tampak seperti bukti dari masalah tersebut. Sebelas tahun kemudian, pada tahun 1890, Percy Heawood menunjukkan bahwa bukti Alfred salah. Peter Guthrie Tait mempresentasikan upaya pembuktian lain pada tahun 1880. Butuh sebelas tahun untuk menunjukkan bahwa bukti Tait juga tidak berhasil. Pada tahun 1891, Julius Petersen bisa menunjukkan hal ini. Ketika dia memalsukan bukti Cayley, Kempe juga menunjukkan bukti untuk masalah yang dia sebut Teorema lima warna. Teorema ini mengatakan bahwa setiap peta tersebut dapat diwarnai dengan tidak lebih dari lima warna. Ada dua batasan: Pertama, setiap negara bersebelahan, tidak ada eksklave. Pembatasan kedua adalah bahwa negara-negara harus memiliki perbatasan yang sama; jika mereka hanya bersentuhan di satu titik, mereka dapat diwarnai dengan warna yang sama. Meskipun bukti Kempe salah, dia menggunakan beberapa ide yang nantinya akan memungkinkan bukti yang benar.

Pada tahun 1960an dan 1970an, Heinrich Heesch mengembangkan sketsa pertama dari sebuah pembuktian dengan komputer. Kenneth Appel dan Wolfgang Haken memperbaiki sketsa ini pada tahun 1976 (Robertson et al. 1996). Mereka mampu mengurangi jumlah kasus yang perlu diuji menjadi 1936; versi selanjutnya dibuat yang hanya mengandalkan pengujian 1476 kasus. Setiap kasus perlu diuji oleh komputer (Appel & Haken 1977).

Pada tahun 1996, Neil Robertson, Daniel Sanders, Paul Seymour dan Robin Thomas memperbaiki metodenya, dan mengurangi jumlah kasus yang harus diuji menjadi 663 kasus. Sekali lagi, setiap kasus perlu diuji dengan komputer.

Pada tahun 2005, Georges Gonthier dan Benjamin Werner mengembangkan bukti formal. Ini adalah sebuah kemajuan, karena memungkinkan untuk menggunakan perangkat lunak pembuktian teorema, untuk pertama kalinya. Perangkat lunak yang digunakan disebut Coq.

Teorema empat warna adalah masalah matematika besar pertama yang dibuktikan dengan bantuan komputer. Karena pembuktiannya tidak dapat dilakukan oleh manusia, beberapa matematikawan tidak mengakuinya sebagai benar. Untuk memverifikasi pembuktian, perlu mengandalkan perangkat lunak dan perangkat keras yang bekerja dengan benar untuk memvalidasi pembuktian. Karena pembuktiannya dilakukan oleh komputer, maka pembuktiannya juga tidak terlalu elegan.

Upaya yang ternyata salah

Teorema empat warna telah terkenal karena menarik sejumlah besar bukti palsu dan pembuktian yang salah dalam sejarahnya yang panjang. Pada awalnya, The New York Times menolak untuk melaporkan bukti Appel-Haken. Surat kabar ini melakukan ini sebagai masalah kebijakan; mereka takut bahwa bukti ini akan terbukti salah seperti bukti-bukti sebelumnya (Wilson 2002, hal. 209). Beberapa bukti membutuhkan waktu yang lama, sampai mereka bisa dipalsukan: Untuk bukti Kempe dan Tait, memalsukannya membutuhkan waktu lebih dari satu dekade.

Contoh tandingan yang paling sederhana pada umumnya mencoba membuat satu wilayah yang menyentuh semua wilayah lainnya. Hal ini memaksa daerah yang tersisa untuk diwarnai hanya dengan tiga warna. Karena teorema empat warna adalah benar, hal ini selalu mungkin; akan tetapi, karena orang yang menggambar peta terfokus pada satu wilayah yang besar, mereka tidak menyadari bahwa wilayah yang tersisa sebenarnya dapat diwarnai dengan tiga warna.

Trik ini bisa digeneralisasikan: Jika warna dari beberapa daerah dalam peta dipilih sebelumnya, menjadi tidak mungkin untuk mewarnai daerah yang tersisa sedemikian rupa sehingga secara total, hanya empat warna yang digunakan. Seseorang yang memverifikasi counterexample mungkin tidak berpikir bahwa mungkin diperlukan untuk mengubah warna daerah-daerah ini. Hal ini akan membuat counterexample terlihat valid, walaupun sebenarnya tidak.

Mungkin salah satu efek yang mendasari kesalahpahaman umum ini adalah kenyataan bahwa pembatasan warna tidak transitif: sebuah wilayah hanya harus diwarnai berbeda dari wilayah yang disentuhnya secara langsung, bukan wilayah yang menyentuh wilayah yang disentuhnya. Jika ini adalah batasannya, graf planar akan membutuhkan warna-warna dalam jumlah yang sangat banyak.

Penyangkalan palsu lainnya melanggar asumsi teorema dengan cara-cara yang tidak terduga, seperti menggunakan daerah yang memiliki beberapa bagian yang terputus, atau tidak mengizinkan daerah dengan warna yang sama bersentuhan pada suatu titik.

Mewarnai peta politik

Dalam kehidupan nyata, banyak negara memiliki eksklave atau koloni. Karena mereka adalah bagian dari negara tersebut, maka mereka perlu diwarnai dengan warna yang sama dengan negara induknya. Ini berarti bahwa biasanya, lebih dari empat warna diperlukan untuk mewarnai peta tersebut. Ketika matematikawan berbicara tentang grafik yang terkait dengan masalah tersebut, mereka mengatakan bahwa grafik tersebut tidak planar. Meskipun mudah untuk memeriksa apakah sebuah graf adalah planar, menemukan jumlah warna paling sedikit yang dibutuhkan untuk mewarnai graf tersebut sangatlah sulit. Ini adalah NP-complete, yang merupakan salah satu masalah tersulit yang ada. Jumlah warna paling sedikit yang dibutuhkan untuk mewarnai sebuah graf dikenal sebagai bilangan kromatiknya. Banyak masalah yang terjadi ketika mencoba menyelesaikan teorema empat warna berhubungan dengan matematika diskrit. Untuk alasan ini, metode dari topologi aljabar sering digunakan.

Perluasan ke peta "non-flat"

Teorema empat warna mengharuskan "peta" berada pada permukaan datar, yang oleh para matematikawan disebut bidang. Pada tahun 1890, Percy John Heawood menciptakan apa yang disebut dugaan Heawood hari ini: Ini mengajukan pertanyaan yang sama dengan teorema empat warna, tetapi untuk objek topologi apa pun. Sebagai contoh, sebuah torus dapat diwarnai dengan paling banyak tujuh warna. Dugaan Heawood memberikan rumus yang berlaku untuk semua objek tersebut, kecuali botol Klein.