Lingkaran unit
Dalam matematika, lingkaran satuan adalah lingkaran dengan jari-jari 1. Persamaan lingkaran satuan adalah x 2 + y 2 = 1 {\displaystyle x^{2}+y^{2}=1}
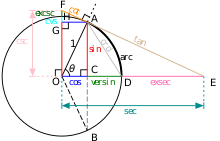
. Lingkaran satuan berpusat di Titik Asal, atau koordinat (0,0). Ini sering digunakan dalam Trigonometri.
Lingkaran Satuan dapat digunakan untuk memodelkan setiap fungsi Trigonometri.
Fungsi trigonometri dalam lingkaran satuan
Dalam lingkaran satuan, dimana t {\displaystyle t}
adalah sudut yang diinginkan, x {\displaystyle x}
dan y {\displaystyle y}
dapat didefinisikan sebagai cos ( t ) = x {\displaystyle \cos(t)=x}
dan sin ( t ) = y {\displaystyle \sin(t)=y}
. Dengan menggunakan fungsi lingkaran satuan, x 2 + y 2 = 1 {\displaystyle x^{2}+y^{2}=1}. , persamaan lain untuk lingkaran satuan ditemukan, cos 2 ( t ) + sin 2 ( t ) = 1 {\displaystyle \cos ^{2}(t)+\sin ^{2}(t)=1}
. Ketika bekerja dengan fungsi trigonometri, sangat berguna untuk menggunakan sudut dengan ukuran antara 0 dan π 2 {\displaystyle \pi \over 2}
radian, atau 0 sampai 90 derajat. Akan tetapi, mungkin saja memiliki sudut yang lebih tinggi dari itu. Dengan menggunakan lingkaran satuan, dua identitas dapat ditemukan: cos ( t ) = cos ( 2 ⋅ π k + t ) {\displaystyle \cos(t)=\cos(2\cdot \pi k + t)}
dan s i n ( t ) = sin ( 2 ⋅ π k + t ) {\displaystyle sin(t)=\sin(2\cdot \pi k + t)}
untuk setiap bilangan bulat k {\displaystyle k}
.
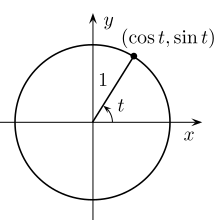
Lingkaran satuan bisa menggantikan variabel untuk fungsi trigonometri.
Pertanyaan dan Jawaban
T: Apa yang dimaksud dengan lingkaran satuan?
J: Lingkaran satuan adalah lingkaran dengan jari-jari 1.
T: Apa persamaan lingkaran satuan?
J: Persamaan lingkaran satuan adalah x^2 + y^2 = 1.
T: Di manakah pusat lingkaran satuan?
J: Lingkaran satuan berpusat di Titik Asal, atau koordinat (0,0).
T: Apa tujuan lingkaran satuan dalam matematika?
J: Lingkaran satuan sering digunakan dalam Trigonometri.
T: Mengapa lingkaran satuan penting?
J: Lingkaran satuan penting karena membantu dalam memahami hubungan antara sudut dan fungsi trigonometri.
T: Berapa jari-jari lingkaran satuan?
J: Jari-jari lingkaran satuan adalah 1.
T: Apa arti penting dari jari-jari lingkaran satuan adalah 1?
J: Pentingnya jari-jari lingkaran satuan adalah 1 adalah untuk menyederhanakan penghitungan dan memudahkan untuk menghubungkan sudut dengan nilai trigonometri.
