Regresi linier
Regresi linier adalah cara untuk menjelaskan hubungan antara variabel dependen dan satu atau lebih variabel penjelas dengan menggunakan garis lurus. Ini adalah kasus khusus dari analisis regresi.
Regresi linier adalah jenis analisis regresi pertama yang dipelajari secara ketat. Hal ini karena model-model yang bergantung secara linear pada parameter-parameter yang tidak diketahui lebih mudah untuk di-fit daripada model-model yang berhubungan secara non-linear dengan parameter-parameternya. Terlebih lagi, sifat statistik dari estimator yang dihasilkan lebih mudah ditentukan.
Regresi linier memiliki banyak kegunaan praktis. Sebagian besar aplikasi masuk ke dalam salah satu dari dua kategori besar berikut ini:
- Regresi linier dapat digunakan untuk menyesuaikan model prediktif ke sekumpulan nilai yang diamati (data). Hal ini berguna, jika tujuannya adalah prediksi, atau peramalan, atau pengurangan. Setelah mengembangkan model seperti itu, jika nilai tambahan X kemudian diberikan tanpa nilai y yang menyertainya, model yang cocok dapat digunakan untuk membuat prediksi nilai y.
- Diberikan variabel y dan sejumlah variabel X1 , ..., Xp yang mungkin terkait dengan y, analisis regresi linier dapat diterapkan untuk mengukur kekuatan hubungan antara y dan Xj , untuk menilai Xj mana yang tidak memiliki hubungan dengan y sama sekali, dan untuk mengidentifikasi himpunan bagian mana dari Xj yang mengandung informasi berlebihan tentang y.
Model regresi linier mencoba membuat jarak vertikal antara garis dan titik-titik data (misalnya residual) sekecil mungkin. Hal ini disebut "menyesuaikan garis dengan data". Seringkali, model regresi linier mencoba meminimalkan jumlah kuadrat residual (kuadrat terkecil), tetapi ada cara lain untuk menyesuaikan. Termasuk meminimalkan "lack of fit" dalam beberapa norma lain (seperti pada regresi least absolute deviations), atau meminimalkan versi penalized dari fungsi least squares loss seperti pada regresi ridge. Pendekatan kuadrat terkecil juga dapat digunakan untuk menyesuaikan model yang tidak linier. Seperti yang telah diuraikan di atas, istilah "least squares" dan "model linear" sangat erat kaitannya, tetapi keduanya bukan sinonim.
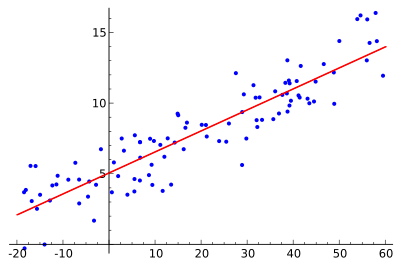
Idenya adalah untuk menemukan kurva merah, titik-titik biru adalah sampel aktual. Dengan regresi linier, semua titik dapat dihubungkan dengan menggunakan satu garis lurus. Contoh ini menggunakan regresi linear sederhana, dimana kuadrat jarak antara garis merah dan setiap titik sampel diminimalkan.
Penggunaan
Ekonomi
Regresi linier adalah alat analisis utama dalam ilmu ekonomi. Misalnya, digunakan untuk menebak pengeluaran konsumsi, pengeluaran investasi tetap, investasi persediaan, pembelian ekspor suatu negara, pengeluaran untuk impor, permintaan untuk memegang aset likuid, permintaan tenaga kerja, dan penawaran tenaga kerja.
Pertanyaan dan Jawaban
T: Apa yang dimaksud dengan regresi linier?
J: Regresi linier adalah cara untuk melihat bagaimana sesuatu berubah ketika hal-hal lain berubah menggunakan matematika. Regresi ini menggunakan variabel dependen dan satu atau lebih variabel penjelas untuk membuat garis lurus, yang dikenal sebagai "garis regresi".
T: Apa keuntungan dari regresi linier?
J: Model-model yang bergantung secara linear pada parameter yang tidak diketahui lebih mudah untuk disesuaikan daripada model-model yang berhubungan secara non-linear dengan parameternya. Selain itu, sifat statistik dari estimator yang dihasilkan lebih mudah ditentukan.
T: Apa saja kegunaan praktis dari regresi linear?
J: Regresi linear dapat digunakan untuk menyesuaikan model prediktif dengan nilai yang diamati (data) untuk membuat prediksi, perkiraan atau pengurangan. Regresi ini juga dapat digunakan untuk mengukur kekuatan hubungan antar variabel dan mengidentifikasi himpunan bagian data yang mengandung informasi berlebihan tentang variabel lain.
T: Bagaimana model regresi linier mencoba meminimalkan kesalahan?
J: Model regresi linear mencoba membuat jarak vertikal antara garis dan titik data (residual) sekecil mungkin. Hal ini dilakukan dengan meminimalkan jumlah kuadrat residual (kuadrat terkecil), kurangnya kecocokan dalam beberapa norma lain (deviasi absolut terkecil), atau meminimalkan versi penalized dari fungsi kerugian kuadrat terkecil (regresi ridge).
T: Apakah mungkin model regresi linier tidak didasarkan pada kuadrat terkecil?
J: Ya, adalah mungkin untuk model regresi linear tidak didasarkan pada kuadrat terkecil tetapi menggunakan metode seperti meminimalkan ketidakcocokan dalam beberapa norma lain (deviasi absolut terkecil) atau meminimalkan versi penalized dari fungsi kerugian kuadrat terkecil (regresi ridge).
T: Apakah "model linear" dan "kuadrat terkecil" sinonim?
J: Tidak, keduanya bukan sinonim. Meskipun keduanya terkait erat, "model linear" secara khusus mengacu pada penggunaan garis lurus, sedangkan "kuadrat terkecil" secara khusus mengacu pada upaya meminimalkan kesalahan dengan memastikan bahwa ada jarak vertikal minimal antara garis dan titik data.
Cari di dalam ensiklopedia